三角関数

三角関数でまずしっかりおさえておきたいのは、やはり \(\sin\) (サイン)、\(\cos\) (コサイン)、\(\tan\) (タンジェント) です。

サインとコサインとは何かを覚えるときに、直角三角形の辺の関係だけで覚えていると応用しにくいです。次のように単位円で考えるようにしましょう。

原点を中心とした半径 1 の円を描いて、原点から \(x\) 軸と反時計回りに \(\theta\) の角度の線を引きます。その円と線が交わったところの \(x\) の値が \(\cos \theta\) で、\(y\) の値が \(\sin \theta \) です。

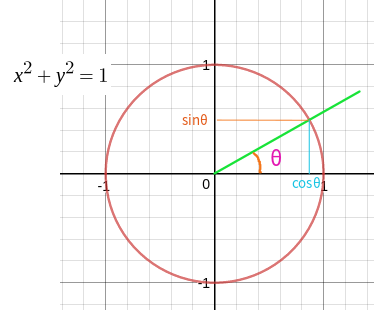
\(\tan \theta\) は、角度 \(\theta\) で引いた上の緑色の直線の傾きです。「傾き」は「x が 1 変化したときの y の変化量」ですから、\( \tan \theta = \displaystyle\frac{\Delta y}{\Delta x} = \displaystyle\frac{\sin \theta}{\cos \theta}\) です。

こうして覚えておけば、\(\cos(- \theta) = \cos \theta\) とか \( \sin(-\theta) = - \sin \theta \) ということは、無理に暗記するまでもなく明らかですね。 ( \(-\theta\) は \(x\) 軸から時計回りに角度 \(\theta\) だけ回すということです)

このことから、直角三角形で斜辺とのなす角度がわかると残りの 2 辺が \(\sin \) と \(\cos\) で表せます。「三角関数に慣れる (1)」

加法定理

\(\sin\)、 \(\cos\)、\(\tan\) の角度の足し算、引き算については、加法定理を覚えましょう。これはとても重要です。

\[ \begin{aligned} \sin (\alpha \pm \beta) &= \sin \alpha \cos \beta \pm \cos \alpha \sin \beta \\ \cos (\alpha \pm \beta) &= \cos \alpha \cos \beta \mp \sin \alpha \sin \beta \\ \tan (\alpha \pm \beta) &= \frac{\tan \alpha \pm \tan \beta}{1 \mp \tan \alpha \tan \beta} \end{aligned} \]

覚え方

サイン「サインコスプラコスサイン」
コサイン「コスコスマイナスサインサイン」
タンジェント「1 マイナス、タンタン分のタンプラタン」

何度も口ずさんで呪文で覚えておくといいです。

2倍角の公式は、加法定理で \( \alpha \)、\(\beta\) を両方とも \(\theta\) と置くことで簡単に導けます。

\[ \begin{aligned} \sin 2\theta &= \sin ( \theta + \theta ) \\ &= \sin \theta \cos \theta + \cos \theta \sin \theta \\ &= 2 \sin \theta \cos \theta \end{aligned} \]

\[ \begin{aligned} \cos 2\theta &= \cos ( \theta + \theta ) \\ &= \cos \theta \cos \theta - \sin \theta \sin \theta \\ &= \cos^2 \theta - \sin^2 \theta \\ &= \cos^2 \theta - ( 1 - \cos^2 \theta ) \\ &= 2 \cos^2 \theta - 1 \end{aligned} \]

これを書き直すと

\[ \cos^2 \theta = \frac{\cos 2\theta + 1}{2} \]

となります。

\(\cos^2\) なんてものが、角度を倍にするだけで「２乗」などの何かと計算が厄介そうな部分が消えてくれるのでありがたいですね。

\(\pi/2\) 位相をズラす

それから、次のように \(\pi/2\) 足したりしたときの \(\sin\) と \(\cos\) の関係も加法定理でわかります。

\(\cos \frac{\pi}{2} = 0\) とか \(\sin \frac{\pi}{2} = 1\) であることを使えば、次のようになります。

\[ \begin{aligned} \sin(\theta + \frac{\pi}{2}) &= \sin \theta \cos \frac{\pi}{2} + \cos \theta \sin \frac{\pi}{2}\\ &= \cos \theta \end{aligned} \]

単位円上で 90° 角度を動かしてみても分かることは分かるのですが、私はうっかり符号を間違えたりすることが多いので、加法定理で間違いがないことを確認するようにしてます。

逆数はそれぞれ \(\sec\)、\(\csc\)、\(\cot\)

正割 (セカント \(\sec\))、余割 (コセカント \(\csc\) )、余接 (コタンジェント \(\cot\)) は日本の高校のテキストではあまり出てこないのですが、アメリカのテキストでは普通に出てきます。

\[ \begin{aligned} \sec \theta &= \frac{1}{\cos \theta}\\ \csc \theta &= \frac{1}{\sin \theta}\\ \cot \theta &= \frac{1}{\tan \theta} \end{aligned} \]

とりあえず読み方と、何の逆数だったかくらいは覚えておきましょう。

尚、コセカントは \(\cosec\) という書き方もありますが、アメリカでは \(\csc\) の方が普通に使われているようです。