行列の基本変形

ここでは 行列の基本変形 について説明します。

内容はとても簡単なことですが、いろんなところで「基本変形すると・・・となるから」などとチョイチョイ出てきますので、しっかり覚えておきましょう。

行列の基本変形には、「行」基本変形と、「列」基本変形があります。

行列の行基本変形

次の三つを行基本変形 (elementary row transformations) または行基本操作 (elementary row operations) といいます。

\(i\)行目と \(j\) 行目を入れ替える \((i \ne j)\)
ある行を \(c\) 倍する \((c \ne 0)\)
\(i\) 行目に、\(j\) 行目の \(c\) 倍を加える \((i \ne j , c \ne 0)\)

中身は簡単です。「ある行とある行を入れ替え」「ある行を何倍かする」「ある行にある行の何倍かを加える」とか。 中学校で習う連立方程式を解くときに、式同士でやるような操作と一緒ですね。

それぞれ、具体例で確認していきましょう。

\(i\) 行目と \(j\) 行目を入れ替える \((i \ne j)\)

次の行列でみてみましょう。

\[ \begin{bmatrix} 1 & 2 & 3 \\ 4 & 5 & 6 \\ 7 & 8 & 9 \end{bmatrix} \]

これの 1 行目と 2 行目を入れ替えると、次のようになります。

簡単なことですね。

紙の上ではヒョイと行を入れ替えるだけなのですが、行列を使ってどうやって「計算」するかみておきましょう。

まず、次のような 単位行列 (identity matrix) を考えます。

\[ \begin{bmatrix} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \end{bmatrix} \]

1 行目と 2 行目を入れ替えるには、次のように単位行列の 1 行目と 2 行目を入れ替えた行列を考えます。

\[ \begin{bmatrix} 0 & 1 & 0 \\ 1 & 0 & 0 \\ 0 & 0 & 1 \end{bmatrix} \]

つまり、単位行列に対して行を入れ替えるという基本変形を行っています。単位行列に基本変形をひとつ行って作った行列を特に 基本行列 (elementary matrix) といいます。

基本行列の表記については「単位行列と基本行列」でもう少し詳しく触れます。

これを元の行列の左から掛け算すると、1 行目と 2 行目が入れ替わります。

念のため、計算手順はこちらです。

ある行を \(c\) 倍する \((c \ne 0)\)

こちらも具体例でみておきましょう。次の行列の 3 行目を 2 倍してみます。

\[ \begin{bmatrix} 1 & 2 & 3 \\ 4 & 5 & 6 \\ 7 & 8 & 9 \end{bmatrix} \xrightarrow{\text{3 行目を 2 倍}} \begin{bmatrix} 1 & 2 & 3 \\ 4 & 5 & 6 \\ 14 & 16 & 18 \end{bmatrix} \]

この計算方法もみておきましょう。

こちらは単位行列の 3 行目の要素を \(c\) にして、左から掛け算します。今回の場合 \(c=2\) です。

\[ \begin{bmatrix} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 2 \end{bmatrix} \begin{bmatrix} 1 & 2 & 3 \\ 4 & 5 & 6 \\ 7 & 8 & 9 \end{bmatrix} = \begin{bmatrix} 1 & 2 & 3 \\ 4 & 5 & 6 \\ 14 & 16 & 18 \end{bmatrix} \]

\(i\) 行目に、\(j\) 行目の \(c\) 倍を加える \((i \ne j , c \ne 0)\)

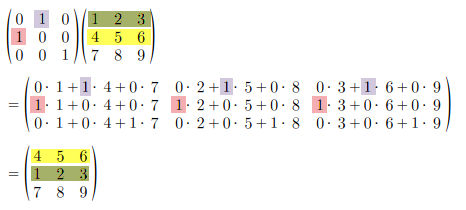
行に関する基本変形の3つ目、「\(i\) 行目に \(j\) 行目の \(c\) 倍を加える」の具体例。「3 行目に 1 行目の 2 倍を加える」と次のようになります。

\[ \begin{bmatrix} 1 & 2 & 3 \\ 4 & 5 & 6 \\ 7 & 8 & 9 \end{bmatrix} \xrightarrow{\text{3 行目に 1 行目の 2 倍を加える}} \begin{bmatrix} 1 & 2 & 3 \\ 4 & 5 & 6 \\ 9 & 12& 15 \end{bmatrix} \]

3 行目の値はそれぞれ、 \( 7 + 1 \cdot 2 = 9\)、\( 8 + 2 \cdot 2 = 12\)、\(9 + 3 \cdot 2 = 15\) で求まるわけですが、こちらも行列の計算としてどうすればいいかみておきましょう。

1 行目を 2 倍して 3 行目に加えるには、次のように単位行列の 3 行目の 1 列目を 2 にします。

\[ \begin{bmatrix} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 2 & 0 & 1 \end{bmatrix} \]

これを元の行列の左から掛けると、3 行目に 1 行目を 2 倍して足し算されます。

念のため、行列の掛け算方法は次の通り。

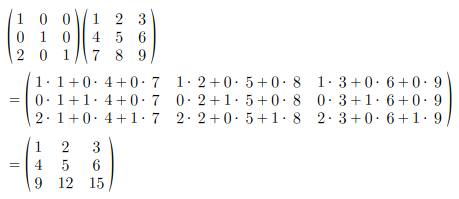
以上でみてきたように、基本行列を行列の左から掛ければ行基本変形できます。

拡大係数行列と掃き出し法で連立方程式を解くとか、あるいは、掃き出し法で逆行列を求めると言う場合には、この行基本変形を用います。

行列の列基本変形

行基本変形と同様のことが「列」に対しても定義されます。

次の三つのルールを列基本変形 (elementary column transformations) または列基本操作 (elementary column operations) といいます。

\(i\)列目と \(j\) 列目を入れ替える \((i \ne j)\)
ある列を \(c\) 倍する \((c \ne 0)\)
\(i\) 列目に、\(j\) 列目の \(c\) 倍を加える \((i \ne j , c \ne 0)\)

こちらは上でみた行の基本変形と同じようなことを、列に対して行います。

列に関する基本変形を行った行列は、基本行列を行列の右から掛ければ得られます。

基本行列を表す記号については、「単位行列と基本行列」をみてください。

以上、行列の基本変形について説明しました。