空間曲線の単位接線ベクトル

ここでは、空間曲線で接線ベクトルがどのように表されるか説明します。

これまで位置ベクトルといえば \(x(t)\), \(y(t)\), \(z(t)\) で

これまで多くの場合では 3 次元空間での位置ベクトルは xyz の直交座標系で位置を決めていたと思います。

例えば、\(t\) を媒介変数として、\(x = x(t)\)、\(y = y(t)\)、\(z = z(t)\) とした場合、曲線上の任意の点の位置ベクトル \(\overrightarrow{r}\) は \(x\)、\(y\)、\(z\) の基底ベクトルをそれぞれ \(\overrightarrow{i}\)、\(\overrightarrow{j}\)、\(\overrightarrow{k}\) として、次のようになりました。

\[ \overrightarrow{r} = x(t) \overrightarrow{i} + y(t) \overrightarrow{j} + z(t) \overrightarrow{k} \]

この場合、 \(\overrightarrow{r}(t)\) を \(t\) で微分すれば接線ベクトルが求められます。なぜなら微分の定義から

\[ \begin{aligned} \frac{ d\overrightarrow{r}}{dt} &= \lim_{\Delta t \to 0} \frac{ \overrightarrow{r}( r + \Delta t) - \overrightarrow{r}(r)}{\Delta t} \end{aligned} \]

ですが、分子の \(\overrightarrow{r}( r + \Delta t) - \overrightarrow{r}(r)\) は明らかに \(t\) が微少変化したときの \(\overrightarrow{r}\) の増分 \(\Delta \overrightarrow{r}\) を表しているからです。

念のため補足すると、これらのベクトルの関係は下の図から \(\overrightarrow{OQ} = \overrightarrow{OP} + \overrightarrow{PQ} \) ですから、 \(\overrightarrow{r}(t + \Delta t) = \overrightarrow{r}(t) + \Delta \overrightarrow{r}\) です。従って \(\Delta \overrightarrow{r} = \overrightarrow{r}(t + \Delta t) - \overrightarrow{r}(t)\) です。

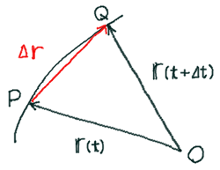
\(\Delta t\) が小さくなれば点 Q は点 P に近付き、\(\Delta \overrightarrow{r}\) は点 P における接線の方向を向くことになります。

\(\displaystyle\frac{d\overrightarrow{r}}{dt} = \overrightarrow{r}'(t)\) は向きは接線の向きですが、大きさは必ずしも単位長 (つまり 1) ではありません。

単位接線ベクトルは、自身の大きさで割った次となります。

\[ \frac{ \overrightarrow{r}'(t) }{ | \overrightarrow{r}'(t) | } \]

曲線上の基準点からの曲線の長さで位置を表す

さて、空間曲線を考えるときには上の方法よりももっと都合の良い方法があります。曲線上のある点を基準として、そこからの長さ \(s\) によって曲線上の点の位置ベクトル \(\overrightarrow{r}(s)\) を定義する方法です。

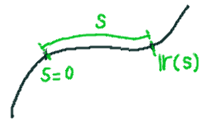
弧長 \(s\) は、\(t=0\) のときの点を基準 \(s=0\) にとると「弧長を求める - パラメータ表示」でみたように、次の式で書けます。

\[ \begin{aligned} s &= \int_0^t \sqrt{ (x'(t))^2 + (y'(t))^2 } dt\\ &= \int_0^t | \overrightarrow{r}'(t) | dt \end{aligned} \]

したがって、\(\displaystyle\frac{ ds }{ dt } = | \overrightarrow{r}'(t) | \) となります。

さて、\(\overrightarrow{r}(s)\) については、\(s\) で微分すると、チェーンルールと上の結果から直ちに次のように変形できます。

\[ \begin{aligned} \frac{ d\overrightarrow{r}(s) }{ds} &= \frac{ d\overrightarrow{r}(t) }{dt} \frac{ dt }{ ds }\\ &= \frac{ \overrightarrow{r}'(t) }{ | \overrightarrow{r}'(t) | } \end{aligned} \]

これは上でみた式と同じですから単位接線ベクトルです。

このように、曲線上の基準点からの弧長で \(\overrightarrow{r}(s)\) をとると、単位接線ベクトルは \(\displaystyle\frac{d \overrightarrow{r}(s)}{ds}\) として直ちに得られます。

図形で位置関係なども確認

上ではパラメータ表示形式時の弧長の求め方などを既知のこととして、単位接線ベクトルを確認しました。ここではついでに \(t\) を介さないで、図を描いて確認しておきます。

曲線上に微小な \(\Delta s\) だけ離れたところに、点 P と点 Q をとります。 P の位置を \(\overrightarrow{r}(s)\) とすると、Q の位置は \(\overrightarrow{r}(s + \Delta s)\) になります。この差を \(\Delta \overrightarrow{r}\) とします。

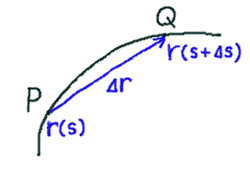
\(\Delta s \to 0\) とするとき、つまり点 Q が点 P に限りなく近付いたとき、直線 PQ は点 P での接線向きになります。(\(s\) の増加方向)

さらに、\(\displaystyle\frac{ | \Delta \overrightarrow{r} | }{\Delta s}\) の大きさは、\(\displaystyle\frac{ | \Delta \overrightarrow{r} | }{\Delta s} = \displaystyle\frac{ \text{弦} PQ}{\text{弧} PQ}\) です。

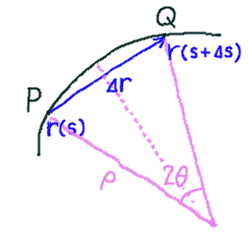
ここで PQ を弧の一部とする円を考え、その中心を O、半径を \(\rho\)、\(\angle POQ\) を \(2\theta\) とします。すると、

\[ \begin{aligned} \frac{ \text{弦} PQ}{\text{弧} PQ} &= \lim_{\theta \to 0} \frac{2 \rho \sin \theta}{2 \rho \theta}\\ &= 1 \end{aligned} \]

よって、確かに \(\displaystyle\frac{d\overrightarrow{r}}{ds}\) は向きが接線向きで、大きさが 1 。つまり単位接線ベクトル \(\overrightarrow{t}\) になりました。

\[\overrightarrow{t}(s) = \frac{d\overrightarrow{r}}{ds}\]