面の向き

ここでは面の向き、つまり表と裏を定義しましょう。

面の向き

面の表と裏は法線ベクトルで定義することにします。 法線ベクトルは裏面から表面に向かうとします。

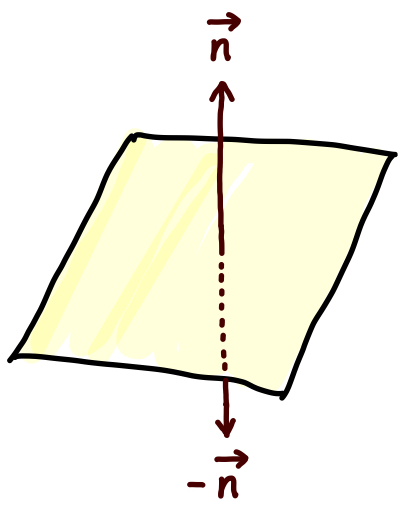
それでは、法線ベクトルはどのように書けるかというと、面上の位置ベクトルを \(u\) と \(v\) をパラメータとして

\[\overrightarrow{r} = x(u,v) \overrightarrow{i} + y(u,v) \overrightarrow{j} + z(u,v) \overrightarrow{k}\]

と書いた時に、法線ベクトル \(\overrightarrow{n}\) は次で求められます。

\[ \overrightarrow{n} = \frac{\cfrac{\partial \overrightarrow{r}}{\partial u} \times \cfrac{\partial \overrightarrow{r}}{\partial v}}{\Big\| \cfrac{\partial \overrightarrow{r}}{\partial u} \times \cfrac{\partial \overrightarrow{r}}{\partial v} \Big\|} \]

これはなぜかというと、次のような図を考えるとわかります。

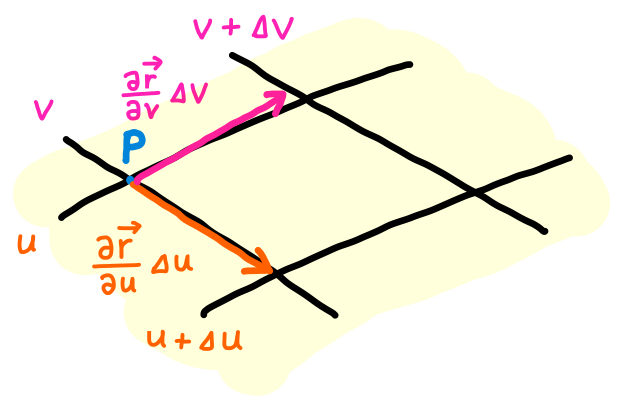
点 \(P\) の位置ベクトルを \(\overrightarrow{r}(u,v)\) とします。このとき、\(u\) が \(\Delta u\) だけ増加した点は、 \(\overrightarrow{r}(u+\Delta u, v)\) です。

\[ \overrightarrow{r}(u+\Delta u, v) = \overrightarrow{r}(u,v) + \frac{\partial \overrightarrow{r}}{\partial u} \Delta u \]

ですから、図のオレンジ色の矢印 (ベクトル) は

\[ \overrightarrow{r}(u+\Delta u, v) - \overrightarrow{r}(u,v) = \frac{\partial \overrightarrow{r}}{\partial u} \Delta u \]

と表されます。

\(v\) 方向についても同様で、ピンク色の部分については、

\[ \overrightarrow{r}(u, v+\Delta v) - \overrightarrow{r}(u,v) = \frac{\partial \overrightarrow{r}}{\partial v} \Delta v \]

法線ベクトル \(\overrightarrow{n}\) はこの２つのベクトル両方に垂直な向きです。

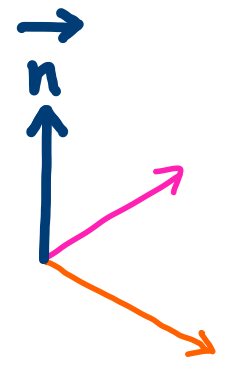
よって、ベクトル積 (外積) を取り、さらに大きさを \(1\) にするために、 その外戚の長さそのもので割れば、上記の式となります。(\(\Delta u \Delta v\) は分子分母でそれぞれ括られて、約分されます)

向きがつけられない面

向きがつけられない面としては、メビウスの帯があります。

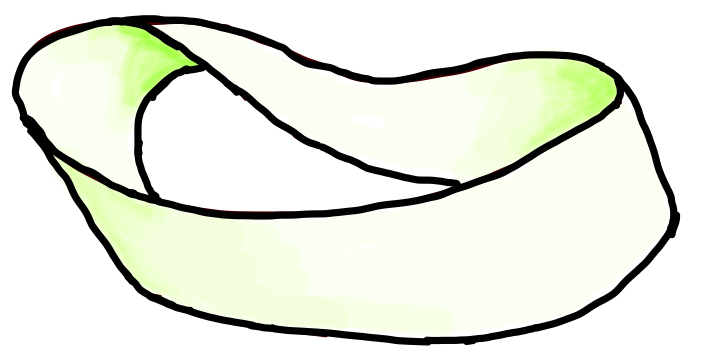
メビウスの帯では、一筆書きで曲面が両面ループできます。

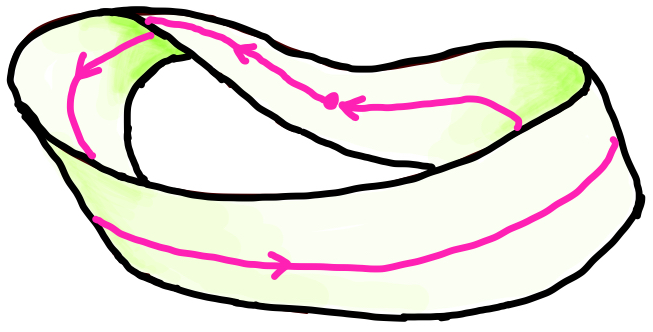
このようなとき、向き付けが不可能であるといいます。