弧長の求め方 - 直交座標表示
ここでは曲線の長さを求める方法を考えます。一般に曲線の長さは弧長 (arc length) といいます。
\(xy\) 平面を考えます。今 \(y=f(x)\) なる関数で表される曲線があるとします。 そして \([a, b]\) での弧の長さを計算してみましょう。
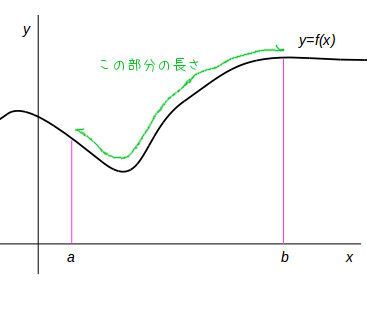
それにはまず、区間 \([a, b]\) を \(n\) 分割して考えます。
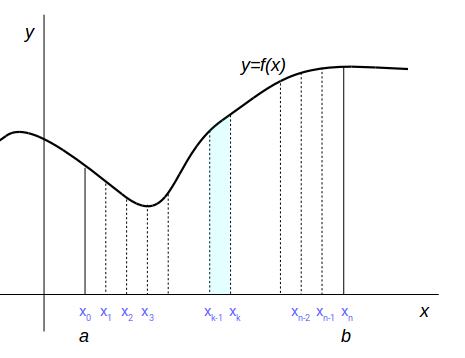
\(k\) 番目の区間 \(x_{k-1}\) から \(x_k\) を考えると、その間の \(y=f(x)\) の弧長は \(\Delta s_k\) は、 下図の三角形 \(ABC\) の斜辺 \(AB\) に近似できます。
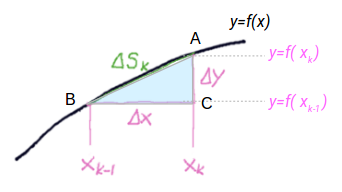
添字 \(k\) のところの \(x\) の幅 \(x_k - x_{k-1}\) を \(\Delta x\)、その区間での \(y\) の増分を \(\Delta y\) と書くと、
\[ \begin{aligned} \Delta s_k &= \sqrt{ (\Delta x)^2 + (\Delta y)^2}\\ &= \sqrt{ 1 + \Big(\frac{\Delta y}{\Delta x}\Big)^2 } \Delta x \end{aligned} \]
したがって、区間 \([a, b]\) の弧長 \(L\) は次のように計算できます。
\[
\begin{aligned}
L &= \lim_{n \to \infty} \sum_{k=1}^n \Delta s_k\\
&=\lim_{n \to \infty} \sum_{k=1}^n \sqrt{ 1 + \Big(\frac{\Delta y}{\Delta x}\Big)^2 } \Delta x\\
&= \int_{a}^{b} \sqrt{ 1 + \Big(\frac{dy}{dx}\Big)^2 } dx\\
&= \int_{a}^{b} \sqrt{ 1 + [ f'(x) ]^2 } dx
\end{aligned}
\]
\[
\begin{aligned}
L &= \int_{a}^{b} \sqrt{ 1 + [ f'(x) ]^2 } dx
\end{aligned}
\]
尚、上で取り上げた微小区間での弧長 \(\displaystyle\lim_{\Delta s\to 0} \Delta s = ds\) は線素といいます。 ベクトル解析などで注釈なしで線素の意味で \(ds\) が出てきたりします。