サラスの公式

ここで紹介する「サラスの公式」は、\(3\) 次の行列の行列式を求めるときに役立ちます。

サラスの公式、あるいは「サラスの方法」(Sarrus' rule) 「サラスの展開」などと呼ばれる公式は、次のようなものです。

サラスの公式 (3x3)

\(3\)次の行列の行列式は、左上から右下に斜めに掛け合わせた成分を足し合わせ、右上から左下に斜めに掛け合わせた成分を引くことで求められる、というものです。

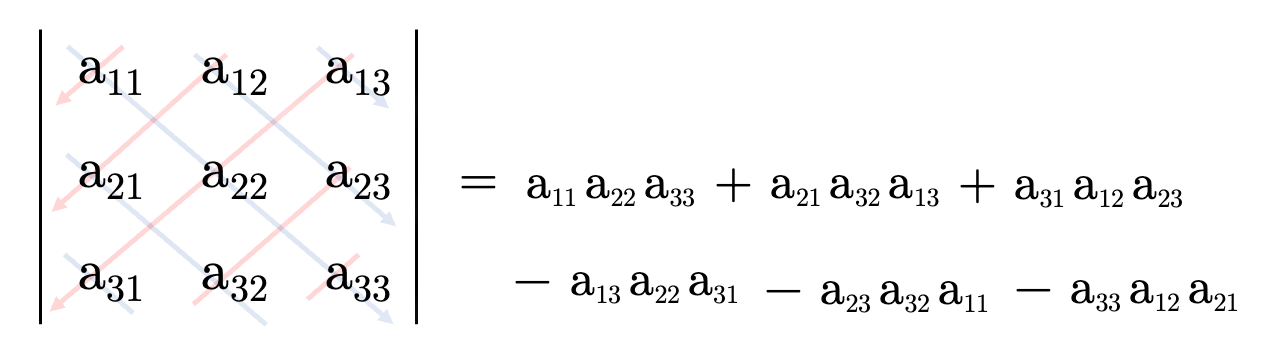
掛け合わせる順番は、次のアニメーションを見てください。青い線で繋いだ成分を掛けて足し、赤い線で繋いだ成分を引き算しています。

例として、次の行列 \(A\) の行列式をサラスの公式で、求めてみましょう。

\[ A = \begin{bmatrix} 1 & 2 & 2\\ 3 & 1 & 0\\ 1 & 3 & 2 \end{bmatrix} \]

公式に沿って、各成分を書き出すと、次のようになります。

\[ \begin{aligned} \det(A) &= 1 \cdot 1 \cdot 2 + 3 \cdot 3 \cdot 2 + 1 \cdot 2 \cdot 0\\ &\space\space - 2 \cdot 1 \cdot 1 - 0 \cdot 3 \cdot 1 - 2 \cdot 2 \cdot 3\\ &= 2 + 18 - 2 - 12\\ &= 6 \end{aligned} \]

たすき掛け (2x2)

\(2\)次の行列の行列式についても、上で見た「サラスの公式」と同様に計算できます。しかし、\(2\)次の場合は、単に「たすき掛け」という言い方をするのが普通です。

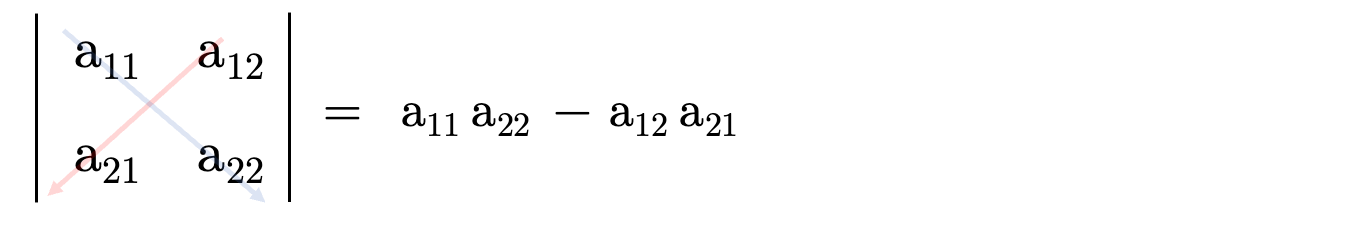
例として、次の行列 \(B\) の行列式を求めてみましょう。

\[ B = \begin{bmatrix} 1 & 2 \\ 3 & 1 \end{bmatrix} \]

公式に沿って、各成分を書き出すと、次のようになります。

\[ \begin{aligned} \det(B) &= 1 \cdot 1 - 2 \cdot 3\\ &= -5 \end{aligned} \]