組立除法

ここでは組立除法 (synthetic division) という計算方法について、やり方を説明します。

具体例で説明します。

多項式 \((3x^3+2x^2-7x+2)\) を \((x-\dfrac{1}{3})\) で割り算するにはどうしたらよいでしょうか。

組立除法を使わないで割り算する方法としては、まず直接、多項式同士の除算として次のように計算する方法があります。

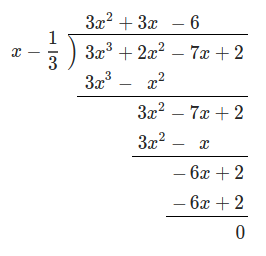
こうした多項式同士の除算は、 Polynomial Long Division といいます。(日本語訳を知らないのですが「多項式長除法」とでも訳していいのかな？）

これは、直感的にわかりやすいのはいいですが、紙に書くと意外と長ったらしくて面倒くさいものです。

そこで組立除法を使ってみましょう。

[手順 1] まず \(3x^3+2x^2-7x+2=0\) の係数 \(3, 2, -7, 2\) を取り出して横に並べ、さらに \(\dfrac{1}{3}\) を左端におき、間に線を引いておきます。

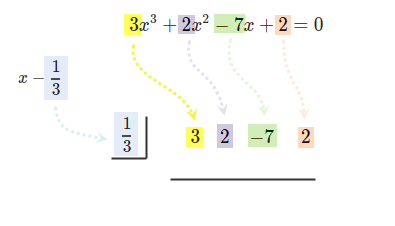
今は \((x-\dfrac{1}{3})\) で割るので \(\dfrac{1}{3}\) ですが、一般に \((x-a)\) で割るなら左端は \(a\) です。

また、割られる多項式が \((x^4+1)\) などの場合は \((1\cdot x^4+0\cdot x^3+0\cdot x^2+0\cdot x+1)\) とみなして、係数は \(1, 0, 0, 0, 1\) と書き並べます。

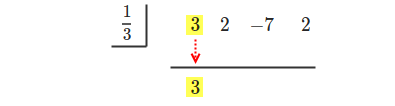
[手順 2] 最初の係数を下に、そのままおろしてきます。

[手順 3] 左端の値と下ろしてきた値を掛け合わせ、その結果を真ん中の行の、下の文字からみて右上に書きます。

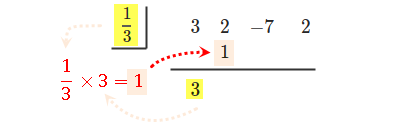
[手順 4] 縦に足し合わせて、下に結果の値を下に書きます。

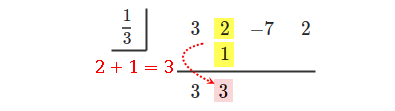
[手順 5] [手順 3] と [手順 4] を繰り返します。

左端の値と下の値を掛け合わせて、真ん中の行に書く。

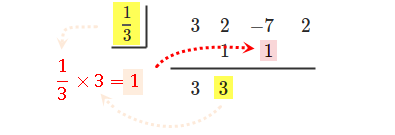
縦に足し合わせて、下に結果を書く。

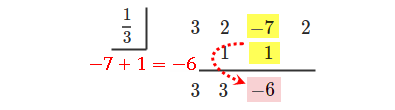
左端の値と下の値を掛け合わせて、真ん中の行に書く。

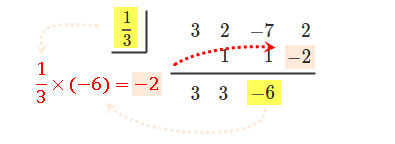
縦に足し合わせて、下に結果を書く。

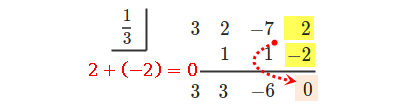
このように繰り替えして、右端まで計算できたら終了です。

この結果、次のような表が得られます。

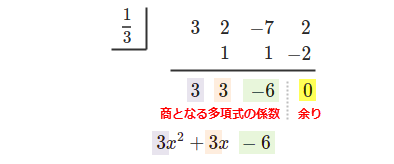
これがどんな意味をもつかというと、一番下の行の右端が余りで、残りの数字は商の多項式の係数になります。

今回の場合は、一番下の行の右端が \(0\) なので、割り切れています。商の多項式の係数が \(3, 3, -6\) であることがわかり、商は \(3x^2+3x-6\) であることがわかりました。

これは確かに上で割り算をした結果とも一致していますね。

多項式を \((x-a)\) で割って、商と余りを計算するのにとても便利な方法ですので、覚えておきましょう。

高次の代数方程式での根を求める際には、有理根定理で根の候補のリストを作って、それから、ここで紹介する組立除法を使って、それぞれが根であるかどうかチェックすることがあります。この場合たくさんの場合を試す必要がありますが、そのような場合には素早く計算できる組立除法が役に立ちます。