因数分解

因数分解 (factorization) というのは、あるものをバラして何かの積として表すことです。

バラしたそれぞれを因数 (factor) といいます。例えば \(A = a \cdot b\) と表されたら、\(a\) と \(b\) は \(A\) の因数というわけです。

ここでは多項式の因数分解を考えます。

まずは中学校位で習う因数分解の公式のおさらいです。

\[ \begin{aligned} x^2 \pm 2xy+y^2 &= (x\pm y)^2\\ x^2-y^2 &= (x-y)(x+y)\\ x^2+(a+b)x+ab &= (x+a)(x+b)\\ x^3\pm 3x^2y+3xy^2\pm y^3 &= (x\pm y)^3\\ x^3 \pm y^3 &= (x\pm y)(x^2\mp xy+y^2) \end{aligned} \]

式をパッとみて、少しは因数分解できそうかどうか少しは思いつかないと、何かと不便ですので、なるべく思い出せるようにしておきたいところです。

\((x \pm y)^2\) や \((x\pm y)^3\) については、「二項定理」も参考にしてください。

\(49^2\) を暗算せよ。

上の公式を、少し「実用的に」使ってみましょう。

\(49^2\) をそのまま素直に計算すると暗算するのは難しいです。その代わり、\(49^2\) を \((50 - 1)^2\) と考えて、\((x - y)^2 = x^2 - 2xy+y^2\) にあてはめてみます。すると、次のように簡単に計算できます。

\[ \begin{aligned} 49^2 &= (50 -1)^2\\ &= 50^2 - 2 \cdot 50 + 1\\ &= 2500 - 100 + 1\\ &= 2401 \end{aligned} \]

こうすれば暗算でも簡単に計算できますね。

高次多項式の因数分解

因数定理を利用して、高次の多項式を因数分解してみましょう。

例として \(P(x) = 2x^4+x^3-19x^2-9x+9\) を因数分解します。因数定理を利用するため \(P(x)=0\) とおきます。そして、この方程式の根 \(a\) を見つけられれば \((x-a)\) が因数となります。

さて、それでは \(2x^4+x^3-19x^2-9x+9 = 0\) の根はどうやって見つければよいでしょうか？当てずっぽうに \(x\) にあれこれ代入して試すのも、なかなかツライものがありますよね。

ここで有理根定理を思い出しましょう。知らないという人は「有理根定理」をみてください。

有理根定理より、\(2x^4+x^3-19x^2-9x+9 = 0\) の根の候補は、次のようにリストできます。

\[ \begin{aligned} x &= \pm\frac{1}{1}, \pm\frac{3}{1}, \pm\frac{9}{1}, \pm\frac{1}{2}, \pm\frac{3}{2}, \pm\frac{9}{2} \\ &= \pm1, \pm3, \pm9, \pm\frac{1}{2}, \pm\frac{3}{2}, \pm\frac{9}{2} \end{aligned} \]

組立除法を使って、\(P(x)\) を \((x-a)\) で除算して余りが \(0\) になる場合を探します。

まず \(a=1\) とすると、

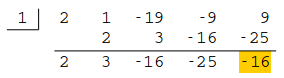
となり、余りが \(-16\) ですから \((x-1)\) は因数ではありません。

次に \(a=-1\) とすると、

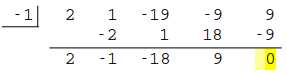
となり、余りが \(0\) ですから \((x+1)\) は因数です。組立除法の商は \(2x^3-x^2-18x+9\) ですから、\(P(x)=(x+1)(2x^3-x^2-18x+9)\) です。

\((2x^3-x^2-18x+9)\) にも上と同様に根の候補が挙げることができるので、\(a=3\) で試すという風に、次々と因数分解して次数を下げていくと、次のように計算していけます。

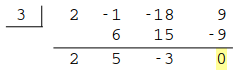
これで \(P(x)=(x+1)(x-3)(2x^2+5x-3)\)。続けて \(a=-3\) を試して、

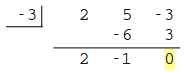
となり、\(P(x)=(x+1)(x-3)(x+3)(2x-1)\) と因数分解できました。

以上、因数分解の方法について説明しました。