ε-δ 論法による極限
微分では極限値を考えるときに、「コレコレを無限に小さく」とか「無限にナントカに近付けた場合」という風なことを考えます。
しかし、エイヤッと「無限に」小さくしてみた、とか、「無限に」エイヤッと近付けたりしてみた、というのでは話が荒っぽくなってしまいます。
そこで、より厳密に極限値を考えるために、ε-δ 論法というのを使います。
ε-δ 論法は 19世紀のドイツの数学者 カール・ワイエルシュトラスによって考案されました。
ε はイプシロン。δ はデルタです。
ε-δ 論法での極限値
ε-δ 論法では\(\displaystyle{\lim_{x \to a}f(x) = L}\) のことを次のように定義します。
もし \(|x-a| < \delta\) ならば、任意の \(\epsilon\) で \(|f(x) - L| \lt \epsilon\) となる、というような \(\delta\) を見つけられるのであれば \(f(x)\) の \(x \to a\) の極限値は \(L\) である
ちなみに、点 \(x = a\) で \(f(x)\) が定義されている必要はありません。
「点 \(x = a\) で \(f(x)\) が定義されている必要はありません」ということはどういうことでしょうか。 例えば次の関数 \(f(x)\) を考えてみましょう。
この関数は \(x = 0\) とすると分母が \(0\) になるので、\(x=0\) では定義されていません。しかし、 \(\displaystyle\lim_{x \to 0} f(x)\) という極限値を考えることはできる、ということです。
任意の \(\epsilon\) というと何をイメージするか分かりにくいですね。\(\epsilon\) については、 「どんなに小さな \(\epsilon\) を考えても」という風に考えておけば良いです。
ですから上の極限の定義を、もう少し噛み砕くと、
どんなに小さな任意の \(\epsilon\) を考えても、\(|x-a| < \delta\) ならば \(|f(x) - L| \lt \epsilon\) になるような \(\delta\) があるなら \(\displaystyle{\lim_{x \to a} f(x) = L}\) である
ということです。
あれやこれやと言い換えて、もとの定義から遠ざかっても良くないので、具体的に問題を解いて理解を深めましょう。
\(\epsilon-\delta\) 法で \(\displaystyle{\lim_{x \to 3}(2x-1)} = 5\) を証明せよ。
ここでは評価する関数 \(f(x) = 2x - 1\) です。これはグラフを書くと下図のような直線のグラフになります。
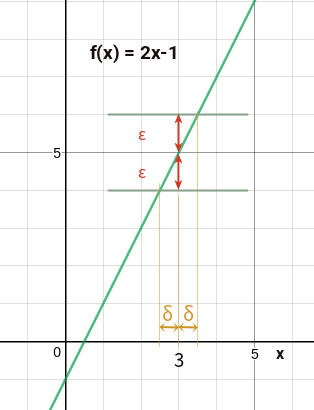
\(\delta\) をどのようにとれば \(| (2x - 1) - 5 | \lt \epsilon\) となるか考えるのですね。
\(0 \lt |x - 3| \lt \delta\) ならば、
\[ \begin{aligned} | (2x - 1) - 5| &= |2x - 6|\\ &= | 2(x - 3)|\\ &= |2| |x - 3|\\ &= 2 |x-3|\\ &\lt 2 \delta \end{aligned} \]
よって、これが \(\epsilon\) より小さいので
\[ 2 \delta \lt \epsilon \]
すなわち、
\[ \delta < \frac{\epsilon}{2} \]
となる \(\delta\) をとれば、\(| (2x - 1) - 5 | \lt \epsilon\) を満たす。
従って \(\displaystyle{\lim_{x \to 3}(2x-1)} = 5\) である。
解答の意味を念のためもう一度みておきます。
もう一度同じ図をみてください。

ここでは \(\epsilon = 1\) として図を描いています。すると、確かに \(\delta = \displaystyle{\frac{\epsilon}{2}} = 0.5\) として、 \(x = 3 \pm 0.5\) の範囲では、極限値 \(5\) から \(\epsilon = 1\) ほども離れていない値をとることがわかりますね。
\(x \to +\infty\) のときの極限については 「ε-δ 論法による極限 (x → ∞)」をみてください。 考え方は一緒ですが、ちょっと違います。