調和振動子と微分方程式

ここでは定数係数の二階線形微分方程式の応用についてみてみましょう。 調和振動子 (harmonic oscillator) です。

まず、どんな状況かというと、次のような模型を考えます。

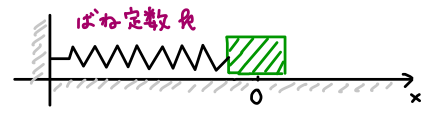
緑色で示した、ある物体があり、それが壁とバネで繋がっています。 物体の質量は \(m\)、バネのバネ定数は \(k\) とします。

この状況で、物体を右方向 (\(x\) の正の方向) に \(x\) だけ引っ張ります。

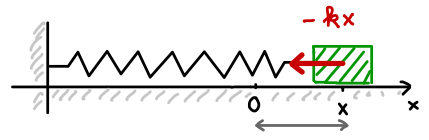
すると、バネが引っ張られるので、物体の位置を元に戻そうとする力が、物体に \(-kx\) だけかかります。 マイナスの符号になっているのは、今、\(x\)のプラスの方向が右向きなのですが、バネが左側についているので、 \(x\)のマイナスの方向になっているからです。

さて今、位置が \(x\) で与えられています。速度というのは位置の時間変化率ですから \(\displaystyle\frac{dx}{dt}\) です。

さらに速さの時間変化率は加速度になりますので、加速度 \(a\) は \(a = \displaystyle\frac{d^2x}{dt^2}\) です。

さて、運動方程式は次のように表されます。

\[F = ma\]

今回の場合に当てはめると、上の状況の運動方程式は次のようになります。

\[ -kx = m \frac{d^2x}{dt^2} \]

整理すると

\[ m \frac{d^2x}{dt^2} + kx = 0 \]

これは、定数係数の2階同次線形微分方程式です。さっそく解いてみましょう。

特性方程式は次の通りです。

\[ \begin{aligned} m \lambda^2 + k &= 0\\ \lambda^2 &= - \frac{k}{m}\\ \therefore \ \lambda &= \pm i \sqrt{\frac{k}{m}} \end{aligned} \]

虚根 \(\lambda = \pm i \sqrt{\displaystyle\frac{k}{m}}\) を持つことから、 上の運動方程式の一般解は次であることがわかります。

\[ \begin{aligned} x(t) &= e^{0\cdot t} \Big( C_1 \cos \sqrt{\frac{k}{m}}t + C_2 \sin \sqrt{\frac{k}{m}}t \Big)\\ &= C_1 \cos \sqrt{\frac{k}{m}}t + C_2 \sin \sqrt{\frac{k}{m}}t \\ &= A \sin \Big(\sqrt{\frac{k}{m}}t + \delta\Big) \end{aligned} \]

式の最後は三角関数の合成公式で \(\sin\) にまとめました。\(\delta\) は \(t=0\) のときの位相 (初期位相) です。 \(A\) は定数の振り幅 (振幅) です。

この結果から、物体の位置は最大振り幅が一定かつ、周期関数である \(\sin\) で表されたので、 単純に行ったり来たりし続けることがわかりました。

一般的に、このように「質点が定点からの距離に比例する引力を受けて運動する系」のことを調和振動子あるいは単振動といいます。