指数関数

指数関数 は「ナントカの何乗」という関数のことです。

例えば「関数 \(f\) が \(2\) の \(x\) 乗なら \(f(x) = 2^x\) 」となりますが、これは指数関数です。ただ、通常、工学の分野でいきなり指数関数といったら、\(e\) の \(x\) 乗のことです。つまり \(f(x) = e^x\) です。

\(e\) は 自然対数の底 で、2.71828 18284 5904... と続く値です。

ネイピア数 とか オイラー数 ともいいます。

ちなみに、\(e\) の覚え方はいろいろあるでしょうけど、「鮒ひと箸ふた箸 (2.71828)、ひと箸ふた箸(1828)。至極おいしい(45904)」なんて覚え方もあります。どう覚えてもいいと思いますが、だいたい 2.718 位ということは覚えておいた方がいいでしょう。

\( f(x) = e^x \) のときに、それを微分しても \(e^x\) です。

\[ \begin{aligned} f(x) &= e^x \\ f'(x) &= e^x \end{aligned} \]

\(f'(x)\) は \(f\) のグラフの傾きになります。\(x=0\) のときは \(f'(0) = e^0 = 1\) ですから、この指数関数のグラフを書いたときに、 \(x=0\) のとき (つまり \(y\) 軸との切片) の傾きは 1 になります。

実際にグラフを書いてみると、次のようになります。

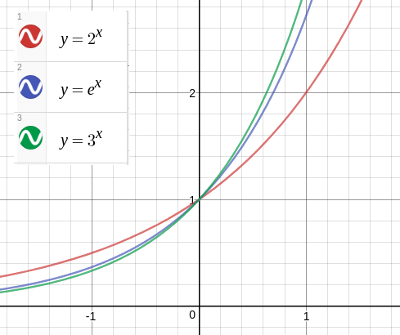
\(e\) は 2.718 位なのでそれをはさむ、\(y=2^x\) と \(y=3^x\) のグラフも描いてます。

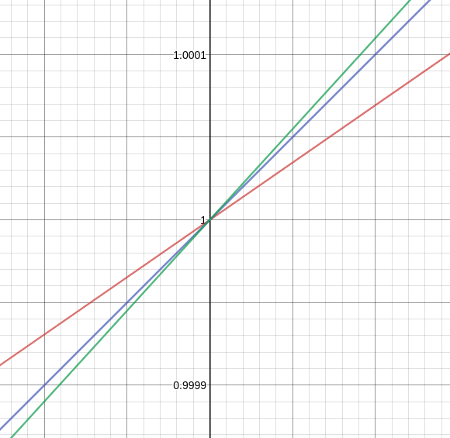
\(y\) 軸との切片のところをグーンとズームしてみてみると、確かに青いグラフ \(y=e^x\) は傾き 1 になってますね。

念のため、\(y=2^x\) について \(x\) で微分すると次のようになります。両辺の自然対数をとって微分してます。

\[ \begin{aligned} y &= 2^x \\ \ln{y} &= x \ln{2} \\ \frac{y'}{y} &= \ln{2} \\ y' &= y \ln{2}\\ &= 2^x \ln{2} \end{aligned} \]

このため、\(y'(0)=2^0 \ln{2} = \ln{2} = 0.693... \) です。

同様に \(y = 3^x\) のときは \(y' = 2^x \ln{3} \) となりますから、\(y'(0) = \ln{3} = 1.0986...\) です。