ベクトルの回転 rot

ベクトル場 \(\overrightarrow{F} = F_1(x,y,z)\overrightarrow{i} + F_2(x,y,z)\overrightarrow{j} + F_3(x,y,z)\overrightarrow{k} \) があるとき、次のベクトルを回転 (rotation) といいます。

\[ \begin{aligned} \text{rot} \overrightarrow{F} &= \nabla \times \overrightarrow{F}\\ &= \begin{vmatrix} \overrightarrow{i} & \overrightarrow{j} & \overrightarrow{k} \\ \cfrac{\partial}{\partial x} & \cfrac{\partial}{\partial y} & \cfrac{\partial}{\partial z} \\ F_1 & F_2 & F_3 \end{vmatrix}\\ &= \Big(\frac{\partial F_3}{\partial y} - \frac{\partial F_2}{\partial z}\Big)\overrightarrow{i} + \Big(\frac{\partial F_1}{\partial z} - \frac{\partial F_3}{\partial x}\Big)\overrightarrow{j} + \Big(\frac{\partial F_2}{\partial x} - \frac{\partial F_1}{\partial y}\Big)\overrightarrow{i} \end{aligned} \]

\(\text{rot}\) の他、\(\text{curl}\) と書くこともありますが、同じ意味です。

「回転」のイメージ。\(\nabla \times \overrightarrow{F}\) は回転軸ベクトル

\(\overrightarrow{F}\) の「回転」が上の式ですよ、と言われても、何かクルクル回ってるわけでもないし、「何でこれが回転なの？何が回ってるの？」と疑問に思うのではないでしょうか。

それでは、実際に回転の計算をしながらイメージをつかみましょう。

例としてベクトル場 \(\overrightarrow{F} = -y \overrightarrow{i}\) を考えます。 \(y\) 軸上の矢印でベクトル場を表すと次のようになってます。

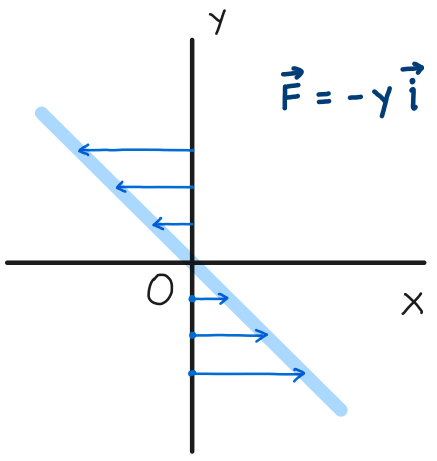
\(y\)方向と\(z\)方向の成分は \(0\) です。\(x\) 方向のベクトルの大きさは、\(y\) の値が大きくなるほど、マイナスの向きに大きくなっています。

この回転 \(\nabla \times \overrightarrow{F}\) は次のように計算できます。

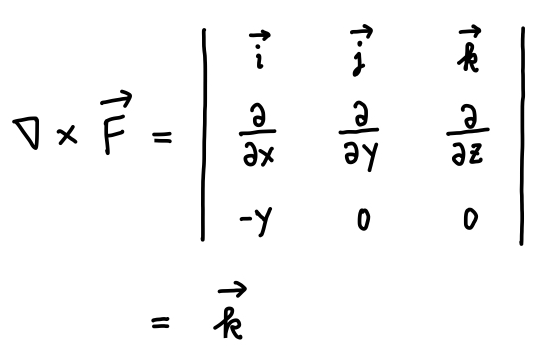
上の計算で、このベクトル場の回転ベクトルは、 \(z\) 軸向きの大きさ \(1\) のベクトルであることがわかりました。

このように回転ベクトルは、ベクトル場が均一ではなく、近くのベクトルに擦り合わされるようにクルッと回る軸の回転軸によって回転を表すのです。ちなみに、向きは反時計回りを正の向きとします。

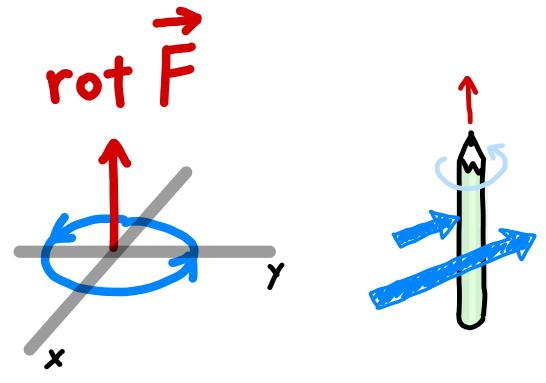
このように回転軸の向きのベクトルの向きと大きさで回転を表すので、上の例では \(x\) 軸方向の成分しかないベクトル場での「回転」(ベクトル) が、\(z\) 軸方向を向いたのです。