余弦定理
余弦定理は三角形の内角の余弦 (コサイン) とそれを挟む2辺と対辺との関係を示したものです。
次の三角形 ABC の内角を \(A\), \(B\), \(C\) として、それぞれの対辺を \(a\)、\(b\)、\(c\) とします。
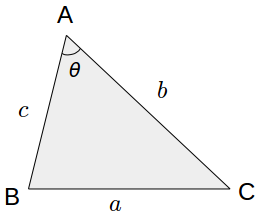
この時に次の関係が成り立つことを余弦定理 (law of cosines) といいます。
\[
a^2 = b^2 + c^2 - 2 b c \cos \theta
\]
特にこの式は「第二」余弦定理といわれます。
余弦定理は三角形の内角の余弦 (コサイン) とそれを挟む2辺と対辺との関係を示したものです。
次の三角形 ABC の内角を \(A\), \(B\), \(C\) として、それぞれの対辺を \(a\)、\(b\)、\(c\) とします。

この時に次の関係が成り立つことを余弦定理 (law of cosines) といいます。
特にこの式は「第二」余弦定理といわれます。
ここまでお読みいただき、誠にありがとうございます。SNS 等でこの記事をシェアしていただけますと、大変励みになります。どうぞよろしくお願いします。