円錐曲線の分類
円錐曲線 (conic curve) というのは円錐面を平面で切り取ってできる、断面の曲線のことです。切り口によって、 円、楕円、双曲線、放物線に分かれます。円錐断面 (conic sections) ともいいます。
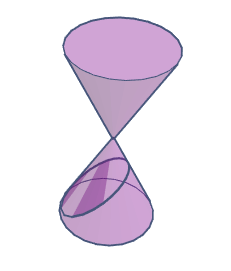
円錐曲線は一般的な形式として、\(xy\) 平面で次の式に表すことができます。
\[
Ax^2 + Bxy + Cy^2 + Dx + Ey + F = 0
\]
ただし、ここで \(A\) から \(F\) は実数で、\(A\)、\(B\)、\(C\) が同時に全て \(0\) にはならないとします。
このとき \(B^2 - 4AC\) を評価することで次のように分類できます。
| 種類 | 判定 |
|---|---|
| 円 | \(B^2 - 4AC \lt 0\) かつ \(B = 0\) かつ \(A = C\) |
| 楕円 | \(B^2 - 4AC \lt 0\) かつ、 \(B \ne 0\) または \(A \ne C\) |
| 双曲線 | \(B^2 - 4AC \gt 0\) |
| 放物線 | \(B^2 - 4AC = 0\) |
これを使うと次のような問題が簡単に解けます。
次の式が表す円錐曲線は何か?
\[
4 x^2 + 8xy + 3y^2 + 2x + 5 = 0
\]
ここでは \(A = 4\)、\(B=8\)、\(C=3\) ですから、\(B^2 - 4AC = 8^2 - 4 \cdot 4 \cdot 3 = 16 \gt 0\) となるので双曲線とわかります。