三角関数の有理式の積分

有理式は多項式の分数の形になる式です。 \(\sin x\) と \(\cos x\) の有理式というのは、次のような式です。

\[ \int \frac{1}{1+\sin x} dx,\ \ \int \frac{\sin^3 x}{1+2 \sin x}dx \]

こうした式を積分するときには、\(t = \displaystyle\tan\frac{x}{2}\) と置くと、\(\sin x\) と \(\cos x\) の部分が次のように、 \(t\) の有理式でかけるようになるので積分しやすくなる、ということになってます。

\[ \begin{aligned} t &= \tan \frac{x}{2}\\ \sin x &= \frac{2t}{1+t^2}\\ \cos x &= \frac{1-t^2}{1+t^2}\\ dx &= \frac{2}{1+t^2} dt \end{aligned} \]

積分しやすくなるのは結構なことなのですが、問題はこの式が少々覚えにくいことです。テストも何もなくて、別に覚えなくてもいいのなら、それに越したことはないんですけどね。

ここでは、丸暗記するのではなく、上の \(\sin x\) と \(\cos x\) を素早く導く方法を説明します。

ちなみに素早くない方法は、加法定理 (というか二倍角の公式など) で地道に式変形することです。\(\sin x = \sin\Big(\displaystyle\frac{x}{2}+\frac{x}{2}\Big)\) と見立てて、 \(\tan \displaystyle\frac{x}{2} \) が出てくるように式変形していけば自然と求まります。

\(t = \tan \displaystyle\frac{x}{2}\) のときの \(\sin x\) と \(\cos x\) を素早く導く

さて、\(t = \tan \displaystyle\frac{x}{2}\) という状況を考えます。そのために次の三角形を考えます。

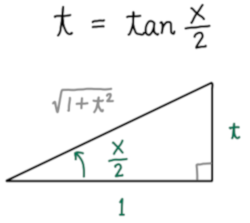
\(\tan \displaystyle\frac{x}{2}\) が \(t\) ということは、上の図の状況ということです。右方向 (\(x\) 軸方向) に \(1\) だけ進んだ時の高さが \(t\) ということです。(タンジェントは傾きですから)

このときの水平線 (\(x\) 軸) と斜辺となす角が \(\displaystyle\frac{x}{2}\) です。

従って、\(\sin \displaystyle\frac{x}{2}\) と \(\cos \displaystyle\frac{x}{2}\) は直ちに次であることがわかります。

\[ \begin{aligned} \sin \frac{x}{2} &= \frac{t}{\sqrt{1+t^2}}\\ \cos \frac{x}{2} &= \frac{1}{\sqrt{1+t^2}} \end{aligned} \]

よって、加法定理から

\[ \begin{aligned} \sin x &= 2 \sin \frac{x}{2} \cos \frac{x}{2}\\ &= 2 \frac{t}{\sqrt{1+t^2}} \frac{1}{\sqrt{1+t^2}}\\ &= \frac{2t}{1+t^2} \end{aligned} \]

これで \(\sin x\) が求まりました。同様に \(\cos x\) も求められます。

\[ \begin{aligned} \cos x &= \cos^2 \frac{x}{2} - \sin^2 \frac{x}{2}\\ &= \frac{1}{t^2 + 1} - \frac{t^2}{t^2 + 1}\\ &= \frac{1-t^2}{1+t^2} \end{aligned} \]

また、\(t = \tan \displaystyle\frac{x}{2}\) の両辺を \(x\) で微分すると、一般に \((\tan x)' = \displaystyle\frac{1}{\cos^2 x}\) ですから、次のように求まります。

\[ \begin{aligned} t &= \tan \frac{x}{2}\\ \frac{dt}{dx} &= \frac{1}{2} \frac{1}{\cos^2 \displaystyle\frac{x}{2}}\\ &= \frac{1+t^2}{2}\\[1.2em] \therefore \ \frac{dx}{dt} &= \frac{2}{1+t^2} \end{aligned} \]

形式的に使いやすい形に書くと、次のようにかけます。

\[ dx = \frac{2}{1+t^2} dt \]

上でしれっと \(\displaystyle\frac{dt}{dx}\) を分子分母ひっくり返しました。一般に関数 \(y = f(x)\) が逆関数を持つ時、 \(y\) が \(x\) について微分可能で \(\displaystyle\frac{dy}{dx}\) が \(0\) でなければ \(x\) は \(y\) について微分可能で、次の式が成り立ちます。

\[ \frac{dx}{dy} = \frac{1}{\displaystyle\frac{dy}{dx}} \]

\(t = \tan \displaystyle\frac{x}{2}\) については、\( (\arctan x)' = (\tan^{-1} x)'= \displaystyle\frac{1}{1+x^2} \) であることを既知とすれば、次のようにできます。

\[ \begin{aligned} t &= \tan \frac{x}{2} \\ x &=2 \tan^{-1} t\\ \therefore \ \frac{dx}{dt} &= \frac{2}{1+t^2} \end{aligned} \]

\(\arctan x\) の微分などについては「逆三角関数の導関数」をみてください。

以上、ここでは \(t = \tan \displaystyle\frac{x}{2}\) の図形的な意味を考えることによって、\(\sin\)、\(\cos\) を手早く導く方法について説明しました。