極限値の基本的な定理

前の記事「極限値」では、極限値とは何か説明しました。ここでは、関数の極限値を求めるために使う定理をみてみましょう。

\(x\) が実数値 \(a\) に限りなく近付く時の極限値

極限値の計算で使う定理は次のようなものになります。

\(a\)、 \(k\) を実数として次が成り立つ。

\(\displaystyle{\lim_{x \to a} k = k} \)
\(\displaystyle{\lim_{x \to a} x = a} \)
\(\displaystyle{\lim_{x \to +0} \cfrac{1}{x} = + \infty} \)
\(\displaystyle{\lim_{x \to -0} \cfrac{1}{x} = - \infty} \)

それぞれ、グラフと具体例をみておきましょう。

\(\displaystyle{\lim_{x \to a} k = k} \)

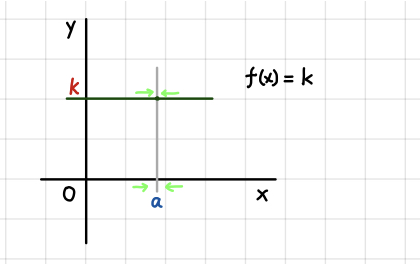
\(a=1\)、\(k=3\) のときは \(\displaystyle{\lim_{x \to 1} 3 = 3}\)。\(3\) は定数で \(x\) によって変わらないので明らかですね。

\(\displaystyle{\lim_{x \to a} x = a} \)

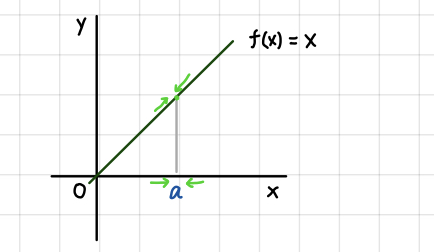
\(a = 5\) のとき \(\displaystyle{\lim_{x \to 5} x = 5}\)。

\(\displaystyle{\lim_{x \to +0} \cfrac{1}{x} = + \infty} \) と \(\displaystyle{\lim_{x \to -0} \cfrac{1}{x} = - \infty} \)

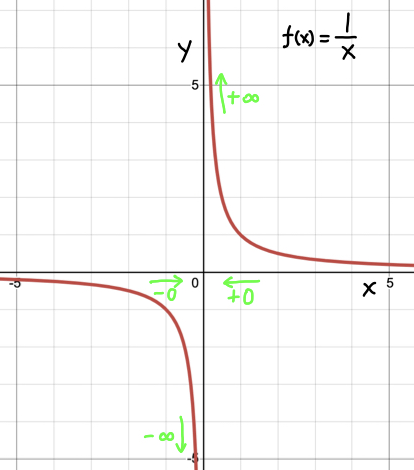
これは右側極限値と左側極限値についてですが、右側 \(x \gt 0\) から \(0\) に近付いたときは、 \(\cfrac{1}{x}\) は正の無限大 \(+\infty\) に発散。左側 \(x \lt 0\) から \(0\) に近付いたときは、負の無限大 \(-\infty\) に発散します。

ある関数 \(f(x)\)、\(g(x)\) の極限値がそれぞれ \(L_1\)、 \(L_2\) と知っている時に、次の関係があります。

\(a\)を実数として、 \(a\)の近くで定義された関数 \(f(x)\)と\(g(x)\)について

\[\lim_{x \to a} f(x) = L_1 \ \ \text{\small{かつ}} \ \ \lim_{x \to a} g(x) = L_2\]

であるとき、以下が成り立つ。

\(\displaystyle{\lim_{x \to a} [f(x) \pm g(x)] = \lim_{x \to a} f(x) \pm \lim_{x \to a} g(x) = L_1 \pm L_2} \)
\(\displaystyle{\lim_{x \to a} [f(x) g(x)] = [\lim_{x \to a} f(x)][\lim_{x \to a} g(x)] = L_1 L_2 }\)
\(\displaystyle{\lim_{x \to a} \frac{f(x)}{g(x)} = \frac{\displaystyle{\lim_{x \to a} f(x)}}{\displaystyle{\lim_{x \to a} g(x)}} = \frac{L_1}{L_2}} \)

(ただし \(g(x) \not = 0\)、\(L_2 \not = 0\))
\(\displaystyle{\lim_{x \to a} \sqrt[n]{f(x)} = \sqrt[n]{\lim_{x \to a} f(x)} = \sqrt[n]{L_1}}\)

(ただし \(n\)が奇数のとき \(L_1 \gt 0\))
\(\displaystyle{ \lim_{x \to a} [k f(x)] = k \lim_{x \to a} f(x) = k L_1}\)

(\(k\) は定数)

例として上で見た定理を駆使して、極限地を求めてみましょう。

次の極限値を求めよ。

\[ \lim_{x \to 2}(2x^3 + 1) \]

上の定理を組み合わせて、計算してみましょう。

\[ \begin{aligned} \lim_{x \to 2}(2x^3 + 1) &= \lim_{x \to 2} 2x^3 + \lim_{x \to 2} 1\\ &= 2 \lim_{x \to 2} x^3 + 1\\ &= 2 [\lim_{x \to 2} x]^3 + 1\\ &= 2 \cdot 2^3 + 1\\ &= 17 \end{aligned} \]

同じ考え方で、関数 \(f(x)\) が多項式で与えられる場合、上の定理から次が成り立つことがわかります。

\(f(x)\)が任意の多項式

\[f(x) = c_0 + c_1x + \cdots + c_n x^n\]

のとき任意の実数 \(a\) に対して次が成り立つ。

\[\lim_{x \to a} f(x) = c_0 + c_1a + \cdots + c_n a^n = f(a) \]

さらに有理関数について、次の定理が成り立ちます。

\(p(x)\) と \(q(x)\) を多項式として、有理関数 \(f(x)\) を次とする。

\[f(x) = \cfrac{p(x)}{q(x)}\]

このとき任意の実数 \(a\) に対して次が成り立つ。

もし \(q(a) \not = 0\) ならば \(\displaystyle{\lim_{x \to a} f(x) = f(a)}\)
もし \(q(a) = 0\) かつ \(p(x) \not = 0\) ならば \(\displaystyle{\lim_{x \to a} f(x)}\) は存在しない

尚、ここでもし \(\displaystyle{\lim_{x \to a} p(x) = 0}\) かつ \(\displaystyle{\lim_{x \to a} q(x) = 0}\) のときは形式的に \(\cfrac{0}{0}\) となります。これは \(\cfrac{0}{0}\) 型の不定形 (indeterminate form of type \(\cfrac{0}{0} \ \)) といって、極限値の存在は別途検討する必要があります。

\(x\) が無限大 \(+\infty\)または無限小 \(-\infty\) になる時の極限値

上では \(x\) が実数値\(a\)に限りなく近付く場合では、左側から近付いた時、右側から近付いた時でそれらが同じであれば極限値が存在する、ということを考えました。

ここでは\(x\)が無限大、または、無限小になる場合の極限値です。

証明については「δ - ε 論法による極限 \(x \to \infty\)」をみてください。

\(k\) を実数として次が成り立つ。

\(\displaystyle{\lim_{x \to -\infty} k = k} \)
\(\displaystyle{\lim_{x \to +\infty} k = k} \)
\(\displaystyle{\lim_{x \to -\infty} x = -\infty} \)
\(\displaystyle{\lim_{x \to +\infty} x = +\infty} \)
\(\displaystyle{\lim_{x \to -\infty} \cfrac{1}{x} = 0} \)
\(\displaystyle{\lim_{x \to +\infty} \cfrac{1}{x} = 0} \)

その他の定理も同様に成り立ちます。

\(a\)を実数として、 \(a\)の近くで定義された関数 \(f(x)\)と\(g(x)\)について

\[\lim_{x \to +\infty} f(x) = L_1 \ \ \text{\small{かつ}} \ \ \lim_{x \to +\infty} g(x) = L_2\]

であるとき、以下が成り立つ。

\(\displaystyle{\lim_{x \to +\infty} [f(x) \pm g(x)] = \lim_{x \to +\infty} f(x) \pm \lim_{x \to +\infty} g(x) = L_1 \pm L_2} \)
\(\displaystyle{\lim_{x \to +\infty} [f(x) g(x)] = [\lim_{x \to +\infty} f(x)][\lim_{x \to +\infty} g(x)] = L_1 L_2 }\)
\(\displaystyle{\lim_{x \to +\infty} \frac{f(x)}{g(x)} = \frac{\displaystyle{\lim_{x \to +\infty} f(x)}}{\displaystyle{\lim_{x \to +\infty} g(x)}} = \frac{L_1}{L_2}} \)

(ただし \(g(x) \not = 0\)、\(L_2 \not = 0\))
\(\displaystyle{\lim_{x \to +\infty} \sqrt[n]{f(x)} = \sqrt[n]{\lim_{x \to +\infty} f(x)} = \sqrt[n]{L_1}}\)

(ただし \(n\)が奇数のとき \(L_1 \gt 0\))
\(\displaystyle{ \lim_{x \to +\infty} [k f(x)] = k \lim_{x \to +\infty} f(x) = k L_1}\)

(\(k\) は定数)

これは \(x \to -\infty\) の場合も同様に成り立ちます。