全確率の公式
ここでは全確率の公式 (Law of Total Probability) に触れておきます。
図を描くと直感的に納得できることなので、場当たり的に導くことも可能かもしれませんが、 ベイズの定理などに絡む問題で良く使いますので、問題を解くツールとしてしっかり意識すると良いです。
さて、次の状況を考えます。
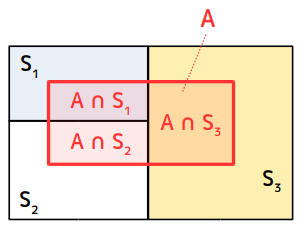
今、全事象 \(S\) が \(S_1, S_2, S_3\) に分割され、かつ \(S_1, S_2, S_3\) はどれも互いに素 (つまり、どれも重ならない) とします。
このとき、ある事象 \(A\) について、
\[ \begin{aligned} A &= A \cap S\\ &= A \cap ( S_1 \cup S_2 \cup S_3 )\\ &= (A \cap S_1) \cup (A \cap S_2) \cup (A \cap S_3)\\ \end{aligned} \]
ここで \((A \cap S_1), (A \cap S_2), (A \cap S_3) \) は互いに素です。
一般に事象 \(X\) と \(Y\) の確率 \(P(X)\) と \(P(Y)\) では次が成り立ちます。
\[ P(X \cup Y) = P(X) + P(Y) - P(X \cap Y) \]
\(X\) と \(Y\) が互いに素、すなわち \(P(X \cap Y) = \emptyset\) のとき
\[ P(X \cup Y) = P(X) + P(Y) \]
したがって \(P(A)\) は次のようにかけます。
\[ P(A) = P(A \cap S_1) + P(A \cap S_2) + P(A \cap S_3) \]
ここでは \(S\) を 3 つに分割しましたが、 \(n\) 個の場合も同様に成り立ちます。
\[ \begin{aligned} P(A) &= P(A \cap S_1) + P(A \cap S_2) + \cdots + P(A \cap S_n)\\ &= \sum^n_{k=1} P(A \cap S_k) \end{aligned} \]
これを全確率の公式といいます。
条件付き確率を用いて表すと、共通部分の確率 \(P(A \cap S_k)\) は
\[ \begin{aligned} P(A | S_k) &= \frac{P(A \cap S_k)}{P(S_k)}\\ \therefore \ P(A \cap S_k) &= P(A | S_k) P(S_k) \end{aligned} \]
と書けるので、全確率の公式は次のようにも書けます。
\[ \begin{aligned} P(A) &= \sum^n_{k=1} P(A | S_k) P(S_k) \end{aligned} \]
それでは、この式を使う問題を考えてみましょう。
ある商品を工場 A と工場 B の 2ヶ所で作っている。毎日、工場 A で 100 個、工場 B で 300 個作っている。 不具合が発生する確率は工場 A が 1% で、工場 B は 5% である。出来上がった商品を任意にひとつ選び、それが欠陥品である確率を求めよ。
工場 A、B 合わせて毎日 100個 + 300個 = 400 個作っている。したがって、商品を一つ選んだときにそれが工場 A で作られている確率 \(P(A)\) は、
\[ P(A) = \frac{100}{400} = 0.25 \]
残りは工場 B で作られているので \(P(B) = 1 - 0.25 = 0.75\) である。
さて、欠陥品である事象を \(D\) とする。
A で作られたもののうち 1% が欠陥品 \(D\) であるから、
\[P(D|A) = 0.01\]
同様に
\[P(D|B) = 0.05 \]
全確率の公式から、全体の欠陥品の確率 \(P(D)\) は次の式で求められる。
\[ \begin{aligned} P(D) &= P(D|A) P(A) + P(D|B) P(B)\\ &= 0.01 \times 0.25 + 0.05 \times 0.75\\ &= 0.04 \end{aligned} \]
念のため、もうひとつ違う方法で確認しておきましょう。
工場 A で作られた 100個のうち欠陥品は 1% であるから、欠陥品は 1 個。工場 B で作られた 300個のうち欠陥品は 5% であるから、欠陥品は 15 個。
したがって、工場 A、B 合わせると、400 個中、16 個が欠陥品であるから
\[ P(D) = \frac{16}{400} = 0.04 \]
新しく出てきた公式を使う方の答えが余計に長いのは、ちょっと拍子抜けですね。 しかし、上のように問題の内容をしっかり整理しておくと、さらに発展でき役に立ちます。
それでは、実際に問題で確かめてみましょう。
ある商品を工場 A と工場 B の 2ヶ所で作っている。毎日、工場 A で 100 個、工場 B で 300 個作っている。 不具合が発生する確率は工場 A が 1% で、工場 B は 5% である。欠陥品がひとつ見つかった場合、それが工場 A で作られていた確率を求めよ。
問題の前提は同じです。上の最初の回答から引き続き考えてみましょう。
求める「欠陥品がひとつ見つかった場合に、それが工場 A で作られていた確率」とは条件付き確率で \(P(A|D)\) である。
\[ \begin{aligned} P(A|D) &= \frac{P(A \cap D)}{P(D)}\\ &= \frac{P(D|A) P(A)}{P(D)}\\ &= \frac{0.01 \times 0.25}{0.04} \\ &= 0.0625 \end{aligned} \]
こうした問題は、ベイズの定理の応用として知られています。
生産量と欠陥の割合に関して按分をとるだけなので、直感的に答えが出てしまうこともあるかもしれませんね。 でも、計算過程が正しいことを確認するためにも記号に慣れ、式を展開できるようにしましょう。
以上、全確率の公式について説明しました。