ベクトル積の大きさは平行四辺形の面積

ここではベクトル積 (クロス積、外積) の大きさは、2 つのベクトルが作る平行四辺形の面積に等しいということについて説明します。

以前の説明ではベクトル \(\overrightarrow{a}\) と \(\overrightarrow{b}\) が張る平行四辺形に、そっと \(\| \overrightarrow{a} \times \overrightarrow{b}\|\) と書いていました。次の図です。

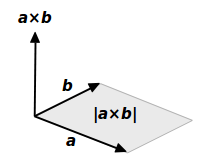
ベクトル積の大きさが、ベクトル \(\overrightarrow{a}\) と \(\overrightarrow{b}\) が作る平行四辺形の面積である、というのはなぜでしょうか。

復習：ベクトル積について

まずは予備知識を復習しておきましょう。

ベクトル積の定義は次の通り。

\[ \begin{aligned} \overrightarrow{a} \times \overrightarrow{b} = (a_2 b_3 - a_3 b_2) \overrightarrow{i} + (a_3 b_1 - a_1 b_3) \overrightarrow{j} + (a_1 b_2 - a_2 b_1) \overrightarrow{k} \end{aligned} \]

行列式を使って書くと次の通り。

\[ \overrightarrow{a} \times \overrightarrow{b} = \begin{vmatrix} \overrightarrow{i} & \overrightarrow{j} & \overrightarrow{k} \\ a_1 & a_2 & a_3 \\ b_1 & b_2 & b_3 \end{vmatrix} \]

「ベクトル積の成分～行列式の表現」も参考にしてください。

このベクトルの大きさは次の通り。

\[ \begin{aligned} \| \overrightarrow{a} \times \overrightarrow{b} \| = \sqrt{(a_2 b_3 - a_3 b_2)^2 + (a_3 b_1 - a_1 b_3)^2 + (a_1 b_2 - a_2 b_1)^2} \end{aligned} \]

復習はこのくらいにして、平行四辺形の面積を考えてみましょう。

\(\overrightarrow{a}\) と \(\overrightarrow{b}\) が作る平行四辺形の面積は？

平行四辺形の面積は (底辺 \(w\)) \(\times\) (高さ \(h\)) で求められます。

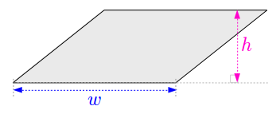
ベクトル \(\overrightarrow{a}\) と \(\overrightarrow{b}\) を平行でない二辺とする平行四辺形を考えます。それらのなす角は \(\theta\) とします。

すると底辺 \(w\) は、ベクトル \(\overrightarrow{a}\) の大きさ \(\| \overrightarrow{a} \|\) です。

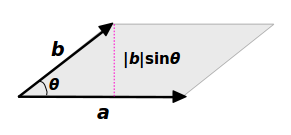
高さ \(h\) はベクトル \(\overrightarrow{b}\) の大きさと角度で \(\|\overrightarrow{b}\| \sin \theta\) と書けます。

急にサイン \(\sin \theta\) が出てきましたね。これがピンと来ない人は「三角関数に慣れる」をみてください。

ベクトルの大きさを表すのに \(\| \overrightarrow{a}\|\) と \(|\overrightarrow{a}|\) という 2 通りで表記していますが、ここでは「ベクトルの大きさ (長さ)」として全く同じものとして解釈してください。図を描くときの問題で一部 \(\|\) が出力できていないだけです。あとで直す予定です。

これらを使うと面積 \(S\) は \( \|\overrightarrow{a}\|\| \overrightarrow{b}\| \sin \theta \) と書けます。

さて、ベクトル \(\overrightarrow{a}\) と \(\overrightarrow{b}\) の内積は \( (\overrightarrow{a} \cdot \overrightarrow{b}) = \|\overrightarrow{a}\|\|\overrightarrow{b}\| \cos \theta \) です。

ベクトルの内積については「ベクトルの内積」をみてください。

三角形の内角 \(\theta\) は \( 0 \lt \theta \lt \pi \) で、この範囲で \(\sin \theta \gt 0 \) です。

従って、

\[ \begin{aligned} \sin \theta &= \sqrt{ 1 - \cos^2 \theta } \\ &= \sqrt{ 1 - \Big( \frac{ (\overrightarrow{a} \cdot \overrightarrow{b} ) }{\| \overrightarrow{a} \| \|\overrightarrow{b}\| } \Big)^2 } \end{aligned} \]

と書けます。

従って、平行四辺形の面積 \(S\) は次のように書き換えられます。

\[ \begin{aligned} S &= \| \overrightarrow{a} \| \| \overrightarrow{b} \| \sin \theta \\ &= \| \overrightarrow{a} \| \| \overrightarrow{b} \| \sqrt{ 1 - \Big( \frac{ (\overrightarrow{a} \cdot \overrightarrow{b} ) }{\| \overrightarrow{a} \| \|\overrightarrow{b}\| } \Big)^2 }\\ &= \sqrt{ \| \overrightarrow{a} \|^2 \| \overrightarrow{b} \|^2 - ( \overrightarrow{a} \cdot \overrightarrow{b} )^2 } \end{aligned} \]

ベクトル \(\overrightarrow{a}\)、\(\overrightarrow{b}\) の成分をそれぞれ、\(\overrightarrow{a} = [a_1, a_2, a_3], \enspace \overrightarrow{b} = [b_1, b_2, b_3] \) とします。すると、上式はさらに次のように書きなおせます。

\[ \begin{aligned} S &= \sqrt{ \| \overrightarrow{a} \|^2 \| \overrightarrow{b} \|^2 - ( \overrightarrow{a} \cdot \overrightarrow{b} )^2 } \\ &= \sqrt{ (a_1^2+a_2^2+a_3^2)(b_1^2+b_2^2+b_3^2) - (a_1b_1+a_2b_2+a_3b_3)^2 }\\ &= \sqrt{ (a_2b_3-b_2a_3)^2 + (a_1b_3 - a_3b_1)^2 + (a_1b_2 - a_2b_1)^2 } \end{aligned} \]

この式は上でみたように \(\| \overrightarrow{a} \times \overrightarrow{b} \|\) の定義そのものです。

以上で二つのベクトルが作る平行四辺形の面積は、それらのベクトル積の大きさに等しいことがわかりました。

ベクトル \(\overrightarrow{a} = \langle2, 0, 0 \rangle\) と \(\overrightarrow{b} = \langle 1, 1, 0 \rangle\) が作る平行四辺形の面積を求めよ。

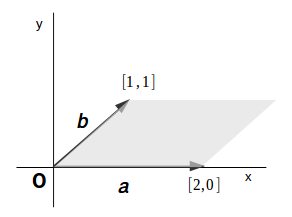
図をみれば (面積) = (底辺) \(\times\) (高さ) = 2 \(\times\) 1 = 2 であることは、すぐにわかりますね。

ここでは試しに、ベクトル積を求めてから、その大きさをみて 2 になるか確かめてみましょう。

\(\overrightarrow{a} = \langle 2, 0, 0 \rangle\) と \(\overrightarrow{b} = \langle 1, 1, 0 \rangle\) のとき、 \(x\) 軸、\(y\) 軸、\(z\) 軸の基本ベクトルをそれぞれ \(\overrightarrow{i}\)、\(\overrightarrow{j}\)、\(\overrightarrow{k}\) とすると、ベクトル積は次のようになります。

\[ \begin{aligned} \overrightarrow{a} \times \overrightarrow{b} &= \begin{vmatrix} \overrightarrow{i} & \overrightarrow{j} & \overrightarrow{k} \\ 2 & 0 & 0 \\ 1 & 1 & 0 \end{vmatrix}\\ &=\begin{vmatrix} 0 & 0 \\ 1 & 0 \end{vmatrix} \overrightarrow{i} + \begin{vmatrix} 0 & 2 \\ 0 & 1 \end{vmatrix} \overrightarrow{j} + \begin{vmatrix} 2 & 0 \\ 1 & 1 \end{vmatrix} \overrightarrow{k} \\ &=2 \overrightarrow{k} \end{aligned} \]

これは \(z\) 軸方向の長さ \(2\) のベクトルですから、\(\| \overrightarrow{a} \times \overrightarrow{b} \| = 2\) です。

確かに「底辺掛ける高さ」として計算した結果と一致しました。

計算方法がわからないときは、ベクトル積全般については「ベクトル積の成分～行列式の表現」を、行列式の計算については「余因子展開による行列式の計算」をみてください。

ベクトル積の大きさは平行四辺形の面積

復習 ： ベクトル積について

\(\overrightarrow{a}\) と \(\overrightarrow{b}\) が作る平行四辺形の面積は？

復習：ベクトル積について