有理根定理

ここでは 有理根定理 (rational root theorem) がどんなものか、簡単に説明します。

あまり聞き慣れない名前かもしれませんが、アメリカだと日本の中学３年生位の９年生位で習うものなので、気楽に構えてくださいね。

有理根定理というのは、次のようなものです。

次のような整数係数の代数方程式を考えます。

\[ a_n x^n + a_{n-1} x^{n-1} + \cdots + a_1 x + a_0 = 0 \]

ここで最高次の係数 \(a_n\) も定数項も \(a_0\) も \(0\) ではないとします。

上の式の有理根 \(x\) を互いに素な整数 \(p\) と \(q\) で、\(x=\dfrac{p}{q}\) と表すと \(q\) は \(a_n\) の因数、\(p\) は \(a_0\) の因数となる、というのが有理根定理です。

ちなみにちょっと復習すると、整数 \(a\) の因数というのは、それを掛け算して \(a\) になる数です。例えば 10 の因数は何かといえば、 \(2\times5=10\) とか \((-1)\times(-10)=10\) などとなるので、\(\pm 1, \pm 2, \pm 5, \pm 10\) となります。

さて有理根定理ですが、具体例を考えるとわかりやすいです。

(例1)

次の方程式を考えます。

\[ 3x^3+2x^2-7x+2=0 \]

この式を満たす \(x\) は何か？という問題を考えます。

有理根定理によって、この \(x\) は

\[ x = \frac{\small{\text{係数項 2 の因数}}}{\small{\text{最高次の係数 3 の因数}}} \]

ということがわかります。したがって、分母が \(\pm1\) または \(\pm3\) 、分子が \(\pm1\) または \(\pm2\) の組み合わせから、次の値が根の候補になります。

\[ \begin{aligned} x &= \pm \frac{1}{1}, \pm \frac{2}{1}, \pm \frac{1}{3}, \pm \frac{2}{3} \\ &= \pm 1, \pm 2, \pm \frac{1}{3}, \pm \frac{2}{3} \end{aligned} \]

これらの候補を上の方程式の \(x\) に代入して \(0\) となれば、それが根ということになります。

値を当てはめるのは、気合で直接代入していっても構いませんが、組立除法を使うのが楽チンです。例えば上の式に \(x=\dfrac{1}{3}\) を代入するには次のようにします。

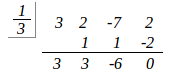
\(x=\dfrac{1}{3}\) を 3乗したりしなくても、計算できてます。

このように代入して式を満たせばそれが根であることがわかります。

候補が多いとそれぞれ代入するのは少々手間ですが、力づくでどうにかなるだけありがたいものです。

以上のように、有理根定理は整数係数の代数方程式で根を推測するのに使うことができます。特に、組立除法と組み合わせて適用して、高次方程式の根を探り当てるのは便利です。