ロジスティック方程式とは

前の記事「人口増加の微分方程式 (マルサスモデル)」では、マルサスモデルについて説明しました。これは人口の増加を表す数理モデルのひとつです。

このモデルはとても簡単な数式で現象を数式化でき大変便利です。

しかしながらマルサスモデルに従うと、例えば人口が際限なく無限に増加するなど、非現実的な面もあります。そこでここでは、何らかの増加の抑制を加えた数理モデルを考えることにしましょう。

病気の拡散

ここでは人口の増加ではなく、病気に罹患した人 \(y(t)\) の増加数を考えてみましょう。全体の人口 \(L\) は一定とします。

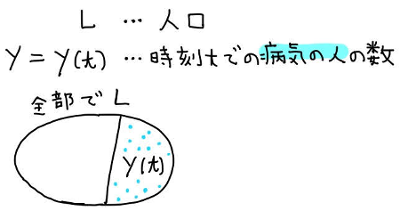
ここでも病人の増加量(数) は、基本的に病人の数に比例する、と考えます。しかし、よく考えてみれば、全員が病気になってしまったら、それ以上病人は増えないので、増加率は 0 になるはずです。

そこで、比例係数を補正して、病人の数が 0 のときは \(k\)、病人の数が \(L\) (つまり全員病気) のときは 0 になるような比例係数 \(K\) を考えましょう。

\(K\) は上のグラフのように、 \(y = 0\) で \(k\)、\(y=L\) で \(0\) となるように直線的に減少することを仮定します。

すると、\(K\) は \(y\) を変数として、傾き \(-\displaystyle\frac{k}{L}\)、縦軸の切片 \(k\) の直線なので、次式で書けます。

\[ K = k \Big( 1 - \frac{y}{L} \Big) \]

これを比例係数として、\(y\) の変化率 (すなわち \(\displaystyle\frac{dy}{dt}\) ) が \(y\) に比例するとすると、次の式が得られます。

\[ \frac{dy}{dt} = k \Big( 1 - \frac{y}{L} \Big) y \]

このような考え方の数理モデルを ロジスティックモデル といいます。

ロジスティックモデルの微分方程式を解く

上で得られた微分方程式 (ロジスティック方程式) を解いて、\(y\) を求めましょう。\(t=0\) のときの \(y\) の値は \( y_0\) とします。

\[ \begin{aligned} &\frac{dy}{dt} = k \Big( 1 - \frac{y}{L} \Big) y\\ &y(0) = y_0 \end{aligned} \]

さて、これを解いていきます。基本方針はやはり変数分離形です。

変数分離形の微分方程式の解き方については「変数分離形の微分方程式の解き方」をみてください。

ロジスティック方程式は基本的な変数分離形として解くことができますが、ベルヌーイの微分方程式としても解くことができます。「ベルヌーイの微分方程式の解き方 (ロジスティック方程式)」も参考にしてください。

後からの計算の都合上、まずは次のように式を変形します。

\[ \begin{aligned} \frac{dy}{dt} &= k \Big( 1 - \frac{y}{L} \Big) y\\ &= \frac{k}{L} y (L - y)\\ \therefore \ \int \frac{L}{y( L - y )} dy &= \int k dt \end{aligned} \]

さて、左辺の被積分関数を部分分数分解して、右辺を積分すると次の式になります。(\(C\) は任意の定数です)

\[ \int \Big( \frac{1}{y} + \frac{1}{L-y} \Big) dy = kt + C \]

部分分数分解の方法については「部分分数分解」を参考にしてください。

\[ \frac{1}{y(L - y)} = \frac{A}{y} + \frac{B}{L-y} \]

とおいて、両辺に \(y(L-y)\) をかけて分母を払うと次の式になります。

\[ 1 = A( L - y ) + By \]

これは \(y\) の恒等式なので、 \(y=0\) とすると \( 1 = A \cdot L \) となるので、\( A = \displaystyle\frac{1}{L} \)。 \(y = L\) とすると \( 1 = B \cdot L \) となるので、\( B = \displaystyle\frac{1}{L}\)。

ゆえに、次の式を得ます。

\[ \begin{aligned} \frac{1}{y(L - y)} &= \frac{1}{L} \Big( \frac{1}{y} + \frac{1}{L-y} \Big) \\ \therefore \ \frac{L}{y(L - y)} &= \frac{1}{y} + \frac{1}{L-y} \end{aligned} \]

これで部分分数分解できました。

上の左辺を積分すると

\[ \begin{aligned} \int \frac{L}{y(L - y)} dy &= \int \Big( \frac{1}{y} + \frac{1}{L-y} \Big) dy \\ &= \ln |y| - \ln | L-y |\\ &= - \ln \Big| \frac{L-y}{y} \Big| \end{aligned} \]

よって、

\[ \begin{aligned} - \ln \Big| \frac{L-y}{y} \Big| &= kt + C\\ \Big| \frac{L-y}{y} \Big| &= e^{-kt-C}\\ \frac{L-y}{y} &= \pm e^{-kt-C} \\ &= \pm e^{-C} \cdot e^{-kt} \\ &= A e^{-kt} \end{aligned} \]

ここで \(A\) は任意の定数です。( \(A = \pm e^{-C}\) ですが、ここに含まれる \(C\) も任意の定数だったので、全体をもう一度任意の定数として置き直しただけです)。

計算を続けましょう。

\[ \begin{aligned} \frac{L}{y} - 1 &= A e^{-kt}\\ \frac{L}{y} &= 1 + A e^{-kt}\\ \therefore \ y &= \frac{L}{1 + A e^{-kt}} \end{aligned} \]

ここで初期値 \(y(0) = y_0\) から \(A\) を求めます。

\[ y(0) = y_0 = \frac{L}{1 + A e^{0}} \]

\(e^{0} = 1\) ですから、

\[ \therefore \ A = \frac{L - y_0}{y_0} \]

以上から、次の式が求められました。

\[ y = \frac{y_0L}{y_0 + (L-y_0) e^{-kt}} \]

ロジスティック方程式を解いて得られた、この解の関数はロジスティック関数と呼ばれます。

\(k = 0.05\)、\(L=100\)、\(y_0 = 5\) としてグラフを描くと次のようになります。

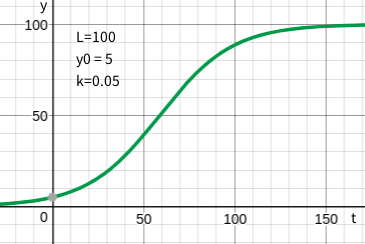
確かに \(y\) が急速に増加する一方ではなく、\(y\) が全数\(L\) に近付くと緩やかに増加しているのがわかります。

ちなみに、ここで登場した個体の全体数 \(L\) は生態学などで環境収容力 (carrying capacity) といいます。

以上、ロジスティック方程式について説明しました。