チェバの定理
いきなりですが、ここでは次の問題を考えてみましょう。
次の三角形 ABC 内に点 O をとる。
直線 AO と 辺 BC の交点を点 D、直線 BO と辺 CA の交点を E、 直線 CO と辺 AB の交点を点 F とします。辺 BC の長さを \(11\) とします。
長さの比は \(AF : FB = 2 : 3\)、\(CE : EA = 4 : 1\) とし、 長さ \(BC = 11 \) とします。
このとき、長さ \(BD\) を求めよ。
この問題はチェバの定理を使うと簡単に解くことができます。
チェバの定理
チェバの定理は上の状況で、次の関係が成り立つことをいいます。
\[
\frac{AF}{FB} \cdot \frac{BD}{DC} \cdot \frac{CE}{EA} = 1
\]
この式の左辺は \(AF\) をスタートとして、\(AF\)、\(FB\)、\(BD\) ・・・のように順番に、分子、分母、分子、分母・・・と置いていった形をしています。
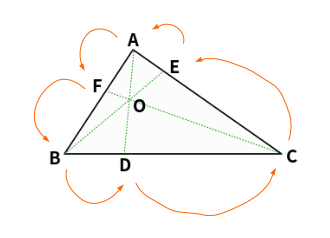
この掛け算が 1 になる、というのがチェバの定理です。
チェバの定理を使って問題を解く
チェバの定理をわかっていれば、上の問題は次のように簡単に解けます。逆に知らないと難しくなってしまうので、しっかり覚えておきましょう。
上の問題では、\(BD + DC = BC\) で \(BC = 11\) ですから \(BD = x\)、\(DC = y\) とおくと \(x + y = 11\) です。
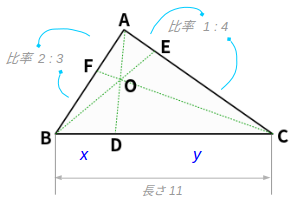
また、\(AF : FB = 2 : 3\)、\(CE : EA = 4 : 1\) をチェバの定理の形に書き直すと、 次のようにかけます。
\[
\begin{aligned}
\frac{AF}{FB} \cdot \frac{BD}{DC} \cdot \frac{CE}{EA} &= 1 \\
\frac{2}{3} \cdot \frac{x}{y} \cdot \frac{4}{1} &= 1 \\
\therefore 8 x &= 3y
\end{aligned}
\]
\(x + y = 11\) と \(8x = 3y\) から \(x\) と \(y\) を計算すると \(x = 3\)、\(y = 8\)。
よって長さ \(BD = 3\) となります。