逆三角関数
通常の三角関数では、角度を与えてそれに応じた値を得ます。
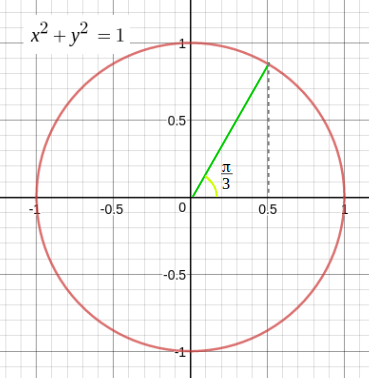
例えば \(y = \cos x\) では、 \(x\) [rad] に角度として \(x = \displaystyle\frac{\pi}{3}\) [rad] を与えれば、\(y = \cos \displaystyle\frac{\pi}{3}\ = \displaystyle\frac{1}{2}\) として \(\cos\) の値が得られます。
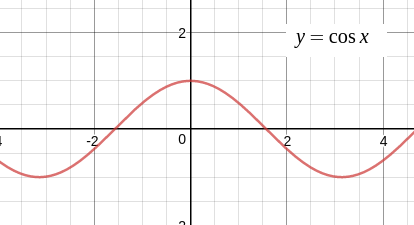
\(y = \cos x\) のグラフは次のようになります。
逆三角関数とは
逆三角関数 (inverse trigonometric function) でやることは、その逆です。値を与えて角度を得ます。
例えば \(\cos x\) に対する逆三角関数である \(y = \arccos x\) では、 \( x = \displaystyle\frac{1}{2}\) という値から、 それに応じた角度として \(y = \displaystyle\frac{\pi}{3}\) [rad] を得ます。
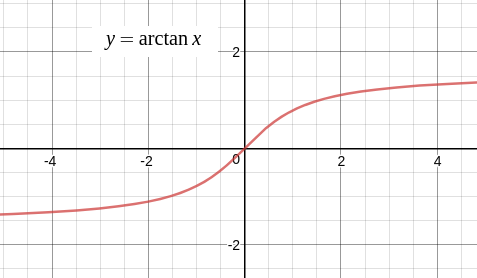
同様に、\(\sin\) の値から角度を得るために \(\arcsin x\)、\(\tan\) に対しては \(\arctan x\) があります。表にまとめると次の通りです。
| 逆三角関数 | 読み方 | やること |
|---|---|---|
| \(y = \arcsin x\) | アークサイン | \(\sin\) の値から角度を得る |
| \(y = \arccos x\) | アークコサイン | \(\cos\) の値から角度を得る |
| \(y = \arctan x\) | アークタンジェント | \(\tan\) の値から角度を得る |
主値とは
\(y = \arccos x\) のグラフは次のようになります。
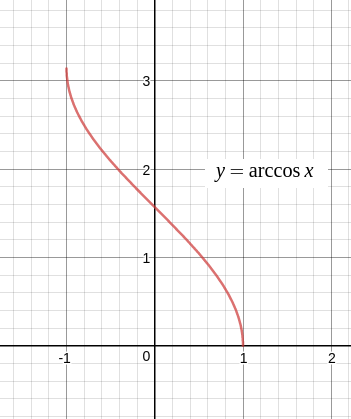
角度として取得できる \(y\) については \( 0 \le y \le \pi \) までの範囲でブチ切られてます。 普通は定義域 (\(x\) 側) で範囲を絞るところですが、ここでは値域 \(y\) をもとに範囲を切っています。
もし、値域で範囲を区切っていないとしたらどうなるか考えてみましょう。
値域に制限がないとき、\( y = \arccos x\) のグラフは下のようになります。
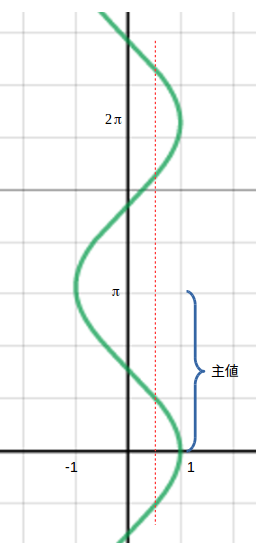
このとき赤い縦線で示した \(x = 0.5\) の時の値は、赤線とグラフの交点が複数あることからわかるように、 複数得られることになります。
一つの入力に対して、複数の値が得られるような関数のことを一般に多価関数 (multivalued function) といいます。 \(y = \arccos x\) は値域を絞らないと多価関数になります。
この場合、値域を限定することによって、一つの入力に対してひとつの値が得られるようにします。 つまり \(y = \arccos x\) を一価関数として扱えるようになります。 こうして選ばれた値域の範囲を主値 (princial value) といいます。
逆三角関数の主値とグラフ
一価関数とする目的だけを考えれば、とりうる値域は無数にあります。例えば 主値として \( 5 \pi \le y \le 6 \pi \) としても確かに一価関数にはなります。 しかし、主値は原点を含み、できるだけプラス側にとるのが基本です。
無駄にややこしく、不揃いにするようなことはせずに、逆三角関数の主値といったら以下の通りです。
\(y = \arccos x\) では主値として \( 0 \le y \le \pi \) をとります。

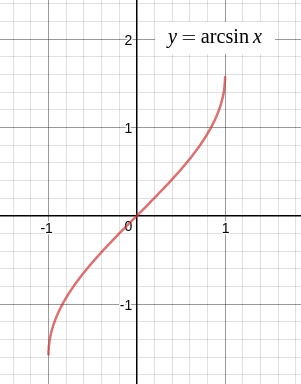
\(y = \arcsin x\) では主値として \( -\displaystyle\frac{\pi}{2} \le y \le \displaystyle\frac{\pi}{2} \) をとります。
\(y = \arctan x\) では主値として \( -\displaystyle\frac{\pi}{2} \lt y \lt \displaystyle\frac{\pi}{2} \) をとります。