偶関数と奇関数の積分
偶関数
偶関数とは?
偶関数 (even function) は全ての \(x\) に対して \(f(-x) = f(x)\) となる関数です。\(x\) のプラスとマイナスを変えても値は同じ、ということです。
つまり、\(x\) の絶対値が同じなら、値が同じになるので、グラフを描くと、 \(y\) 軸に対して線対称です。
\(f(x) = x^{n}\) の時、\(n\) が偶数ならば \(f(-x)=f(x)\) になります。
例えば \(f(x)=x^2\) なら、ご存知の通り、下のようなグラフになります。
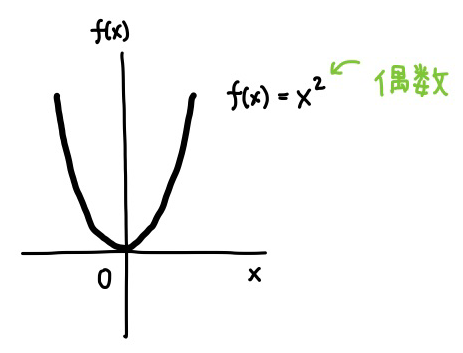
この場合、\(f(x) = f(-x)\)、つまり \(x\) のプラスとマイナスを変えても値は同じですから、これは偶関数です。
偶関数の積分
\(f(x)\) が偶関数である時、\(-L\) から \(L\) までの積分を考えましょう。このとき、
\(f(x)\) が偶関数の時
\[ \int_{-L}^{L} f(x) dx = 2 \int_{0}^{L} f(x) dx \]
となります。
これは面積で考えると明らかです。
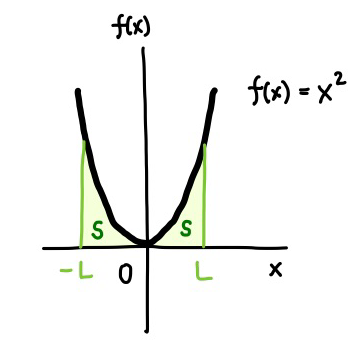
いま、 \(x\) が \(0\) から \(L\) までの面積を \(S\) とすると、
\[ S = \int_0^L f(x) dx \]
です。グラフは \(y\) 軸に対して線対称ですから、\(-L\) から \(0\) までの面積も \(S\) です。
したがって、\(-L\) から \(L\) までの面積は、\(S\) の2倍ですから、
\[ \int_{-L}^{L} f(x) dx = 2 \int_{0}^{L} f(x) dx \]
が成り立ちます。
奇関数
奇関数とは?
奇関数 (odd function) というのは、全ての \(x\) に対して \(f(-x) = -f(x)\) となる関数です。
グラフは原点に対して点対称になります。
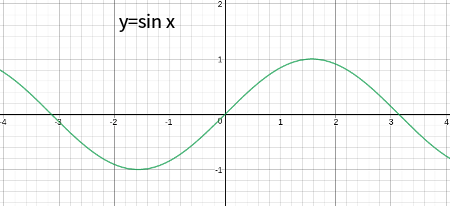
\(f(x) = x^{n}\) の時、\(n\) が奇数ならば \(f(-x)=-f(x)\) ですから、\(f(x)\) は奇関数になります。
例えば \(f(x)=x\) や \(f(x) = x^3\) なら、下のようなグラフになります。
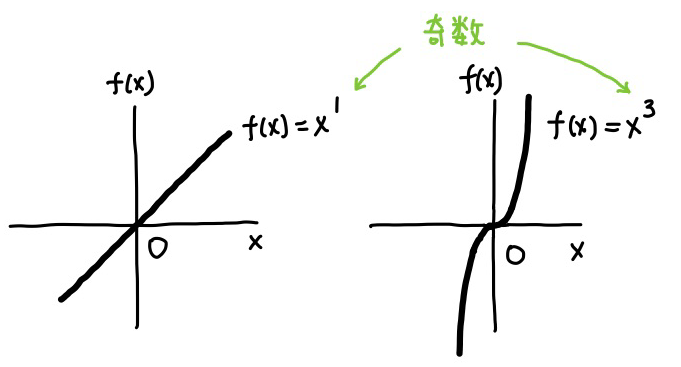
この場合、\(f(-x) = -f(x)\) ですから、これは奇関数です。
奇関数の積分
\(f(x)\) が奇関数である時、\(-L\) から \(L\) までの積分を考えましょう。このとき、
\(f(x)\)が奇関数の時
\[ \int_{-L}^{L} f(x) dx = 0 \]
となります。これも面積で考えると明らかです。
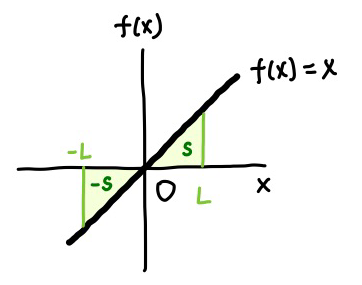
いま、 \(x\) が \(0\) から \(L\) までの面積を \(S\) とすると、
\[ S = \int_0^L f(x) dx \]
です。グラフは \(y\) 軸に対して点対称ですから、\(-L\) から \(0\) までの面積は、符号が逆になり \(-S\) です。
したがって、\(-L\) から \(L\) までの面積は、
\[ \begin{aligned} \int_{-L}^{L} f(x) dx &= \int_{-L}^{0} f(x) dx + \int_{0}^{L} f(x) dx\\ &= -S + S\\ &= 0 \end{aligned} \]
が成り立ちます。
偶関数と奇関数の積
偶関数と奇関数の積については、次のようになります。
- 奇関数 \(\times\) 奇関数 = 偶関数
- 奇関数 \(\times\) 偶関数 = 奇関数
- 偶関数 \(\times\) 偶関数 = 偶関数
例えば、偶関数 \(f(x) = x^2\) と奇関数 \(g(x) = x^3\) をかけると、
\[ \underbrace{x^2}_{\text{偶関数}} \times \underbrace{x^3}_{\text{奇関数}} = \underbrace{x^5}_{\text{奇関数}} \]
となります。
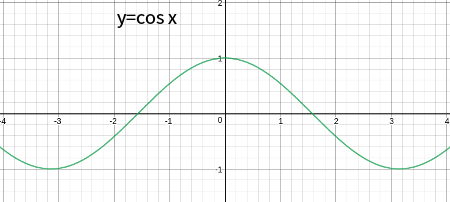
\(f(x) = x^n\) のような単純な場合だけで成り立つのではなく、\(\sin x\) や \(\cos x\) などでも成り立ちます。 \(\cos\) は偶関数、\(\sin\) は奇関数ですから、その積である \(\cos x \cdot \sin x\) は奇関数になります。 このことから、次のような積分は直ちに答えが \(0\) である、とわかります。
こんな風に、一見複雑そうな関数の積分でも、ひと目でわかるのは、計算が楽になってとても便利ですね。