面積素とパラメータ (曲面 \(z=g(x,y)\) の場合)

前回の記事「面積素とパラメータ」では、曲面 \(S\) を次の式としていました。

\[ \overrightarrow{r}(u,v) = x(u,v) \overrightarrow{i} + y(u,v) \overrightarrow{j} + z(u,v) \overrightarrow{k} \]

これは、曲面 \(S\) 上の任意の点を位置ベクトル \(\overrightarrow{r} = \langle x(u,v), y(u,v), z(u,v) \rangle\) としていることと同じです。「\(u\) と \(v\) を使って、 \(x, y, z\) 座標を何らかの関数 \(x(u,v), y(u, v), z(u,v)\) で書く」と言ってるわけです。

一般的に状況を説明するにはこれで全く問題ないのですが、実際に何かの問題を解くには、\(x, y, z\) をもっと具体的に書いておいた方が便利です。

そこで、\(u, v\) の関数 \(x(u,v)\) は単純に \(x(u,v) = u\)、関数 \(y(u,v)\) も \(y(u,v)=v\) とします。こうすると \(u, v\) は \(x, y\) そのものになったので、上の式で \(u, v\) を \(x, y\) に書き換え、 \(z\) は \(x, y\) の関数 \(g(x,y)\) で、 \(z=g(x,y)\) としておきます。

\(z=g(x,y)\) は曲面を表します。 \(xyz\) 直交座標系で \(xy\) 平面に対応して、山の高さ \(z\) が \(z=g(x,y)\) という関数で表されているイメージです。この曲面を \(S\) とします。

面積素

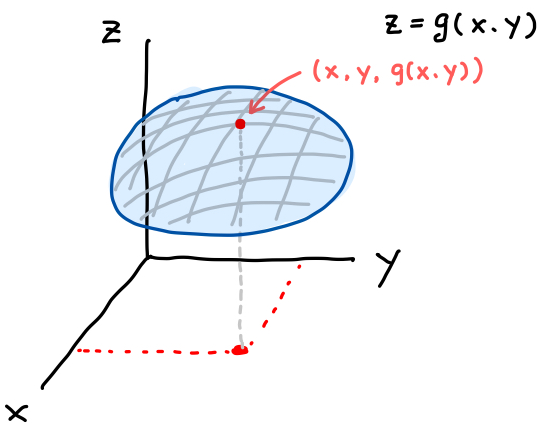
この曲面 \(S\) は、\(S\) 上で微分可能であるために、滑らかな曲面を考えます。

この曲面上の点の位置ベクトルは \(\overrightarrow{r} = \langle x, y, g(x,y) \rangle\) です。

上の説明では「\(uv\)平面」でパラメータが動き回る平面を考えましたが、普通に \(xy\) 平面上に独立変数 \(x, y\) のとる領域を考えればよいことになります。この領域を \(D\) とします。

\(D\) は \(S\) の \(xy\) 平面への正射影になります。

面積素

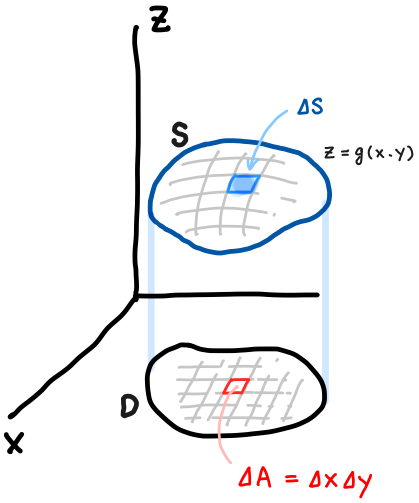
\(x, y\) の領域もひとまとまりの滑らかな領域を考えます。

\(xy\) 平面での \(D\) の面積素は \(\Delta A = \Delta x \Delta y\) です。

上で見たように、面積素 \(\Delta S\) と \(\Delta A\) の関係は次の通りでした。(\(u, v\) を \(x, y\) に置き換えます)

\[ \Delta S = \Big| \frac{\partial \overrightarrow{r}}{\partial x} \times \frac{\partial \overrightarrow{r}}{\partial y} \Big| \Delta A \\ \]

\(\overrightarrow{r} = \langle x, y, g(x,y) \rangle\) をあてはめて、ベクトル積を計算してみましょう。

\[ \begin{aligned} \frac{\partial \overrightarrow{r}}{\partial x} &= \Big\langle 1, 0, \frac{\partial g}{\partial x} \Big\rangle \\ \frac{\partial \overrightarrow{r}}{\partial y} &= \Big\langle 0, 1, \frac{\partial g}{\partial y} \Big\rangle \end{aligned} \]

ですから、これらのベクトル積 (外積) は次のように計算されます。

\[ \begin{aligned} \frac{\partial \overrightarrow{r}}{\partial x} \times \frac{\partial \overrightarrow{r}}{\partial y} &= \begin{vmatrix} \overrightarrow{i} && \overrightarrow{j} && \overrightarrow{k}\\ 1 && 0 && \cfrac{\partial g}{\partial x}\\ 0 && 1 && \cfrac{\partial g}{\partial y} \end{vmatrix}\\ &= - \frac{\partial g}{\partial x} \overrightarrow{i} - \frac{\partial g}{\partial y} \overrightarrow{j} + \overrightarrow{k} \end{aligned} \]

このベクトル積の大きさは次の通りです。

\[ \begin{aligned} \Big| \frac{\partial \overrightarrow{r}}{\partial x} \times \frac{\partial \overrightarrow{r}}{\partial y} \Big| &= \sqrt{\Big(\frac{\partial g}{\partial x}\Big)^2 + \Big(\frac{\partial g}{\partial y}\Big)^2 + 1} \end{aligned} \]

このベクトル積は曲面の法線ベクトルになります。「曲面 \(z=g(x,y)\) の法線」もみてください。

直方体の対角線の長さは辺の長さを \(a, b, c\) として \(\sqrt{a^2+b^2+c^2}\) ですね。

面積素

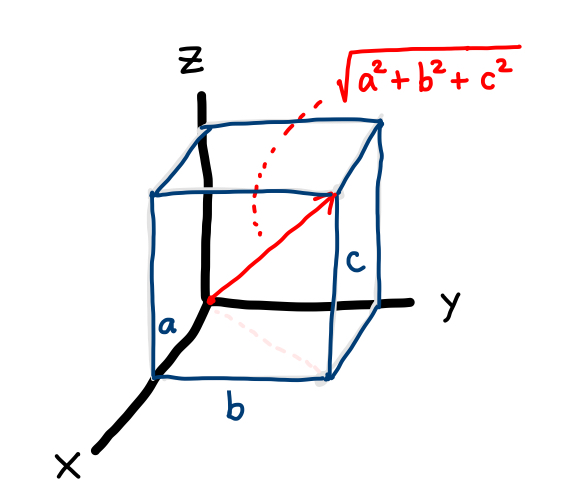
ここでは \(a = -\displaystyle\frac{\partial g}{\partial x}, b = -\displaystyle\frac{\partial g}{\partial y}, c = 1\) ですから、ベクトル積の大きさは上の通りになります。

つまり、\(xy\) 平面上の面積素 \(\Delta A\) と、それに対応する曲面上の面積素 \(\Delta S\) の関係式は次のようにかけることがわかりました。

\[ \begin{aligned} \Delta S &= \Big| \frac{\partial \overrightarrow{r}}{\partial x} \times \frac{\partial \overrightarrow{r}}{\partial y} \Big| \Delta A \\ &= \sqrt{\Big(\frac{\partial g}{\partial x}\Big)^2 + \Big(\frac{\partial g}{\partial y}\Big)^2 + 1} \ \ \Delta A \end{aligned} \]

面積素

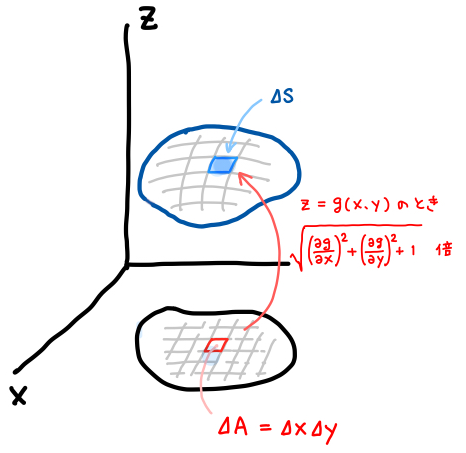
この関係式によって、曲面 \(S\) での面積分の計算をするときも、曲面上で直接積分するかわりに、\(xy\) 平面への正射影を利用して \(S\) の面積分の値を計算できるようになります。