条件付き確率のコツ

ここでは条件付き確率を理解するためのコツ、勘所について説明します。

確率の復習から

はじめに条件付きではない「普通の」確率について復習しましょう。

具体的にサイコロ問題で考えます。

この確率を求めるには 「出る可能性のある全ての目」を分母とし、分子を「偶数が出る場合の数」を数えて求めます。

「出る可能性のある全ての目」は 1, 2, 3, 4, 5, 6 の 6 通りで、「偶数が出る場合の数」は 2, 4, 6 の 3 通りですね。

このため、次のように計算して、確率は 0.5 と計算できます。

これを集合を表す図で確認しましょう。

計算の分母となる「出る可能性のある全ての目」は出る目を要素 (元) として、次のように描けます。この要素の数が分母になるのですね。

そのうち、確率を求めたい偶数の目は、次の囲んだ部分です。この囲んだ部分の要素数が分子になります。

これが確率の基本的な考え方です。

条件付き確率の考え方

さて、それでは上と似たような問題で、条件付き確率を考えてみましょう。

問題文を良く読んでみましょう。

「サイコロを 1 回振ったとき、出た目が 3 より大きいことがわかった」ということは、 サイコロを振って、「出た目が 3 より大きいところまでは分かっているものとする」 ということです。

そして、「それが偶数である確率」 ということは、既に分かっている「3 より大きい」という条件に加えて 「偶数である」という条件も満たす場合の確率を考えなさい、ということです。

文字で書くと次のようになります。

ごちゃごちゃして、ちょっと分かりにくくなってきました。

そこで、図を考えてみましょう。

「3 より大きいことは分かっている」とするわけですから、サイコロのでる目は他にあっても、考える範囲は次の部分だけでいいことになります。

さらに「偶数である」という囲みも重ねてみます。

本来は、上でみたようにサイコロの目の確率は「出る可能性のある全ての目の数」を分母にして考えるのでした。

しかし、今回は「3 より大」という条件があるので、分母は肌色部分の要素数だけでいいことになります。

そしてその範囲内で、「偶数」の確率を求めるのですから、肌色部分に含まれる「偶数」の場合の数を分子にして計算すれば良いことになります。

このことから、求める確率は次のように計算できます。

ここでみたように、「条件付き確率」というのは、条件によって分母となる集合を切り替えて計算する確率のことなのです。

記号と図を使うと、もっと複雑な状況に対応できる

さて、上の問題はサイコロを一回振るときの目の数なので、ひとつふたつ・・・と、数え上げればそれで答えが出せます。

ところが、数が多くて数え切れないとか、 あるいは、条件が何かの確率として与えられる時とか、 場合によってはひとつひとつを数え上げることができない時があります。

そのような状況に対応するためにはどうしたらよいでしょうか。

そのときには、上のような「図」と「集合を表す記号」で計算の手順を理解しておくと対応できる幅が広がります。

それではもう一度同じ問題を考えて、図と記号で考えてみてみましょう。

まず、それぞれの条件を記号を使って定義しておきましょう。

ここでは 「3 より大である」という条件を \(A\)、「偶数である」という条件を \(B\) とします。

要素は消しちゃいます。書いてなくても空っぽではなく、そこにいくつか要素があると考えます。

A と B の重なりの部分である、「A かつ B」は A ∩ B と書きます。

「A の確率」は P(A) と書きます。同様に「B の確率」は P(B)、「A かつ B の確率」は P(A∩B) と書きます。

一般的に次のように A と B があるとします。また全ての要素を含む全体の囲みを U とします。

このとき、それぞれの確率は次の囲みの中の要素の数に対応します。

A の確率 P(A)

要素の数を \(n\) で表して、「A の要素の数」を \(n(A)\)、「全ての要素の数」を \(n(U)\) と書くと、

\[ P(A) = \frac{n(A)}{n(U)} \]

とかけます。

同様に B の確率 P(B) は次の部分です。

よって要素数 \(n\) を使い式で書くと

\[ P(B) = \frac{n(B)}{n(U)} \]

A ∩ B の確率 P(A ∩ B) は

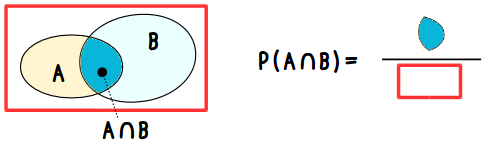
\[ P(A \cap B) = \frac{n(A \cap B)}{n(U)} \]

さて、条件付き確率を図で表すとどうなるでしょうか。

特に今回の場合、すなわち「 A であることがわかっているときの B の確率」は上でみたように

の部分でした。A であるときの B の確率は P(B|A) と書き次のようになります。

よって、要素数の式で書くと次のようになります。

これを確率 \(P\) の式で書き直すと、次のようになります。

\[ \begin{aligned} P(B | A) &= \frac{n(A \cap B)}{n(A)}\\ &= \frac{ P(A \cap B) \cdot n(U) }{ P(A) \cdot n(U)}\\ \end{aligned} \]

これらが条件付き確率を考えるときのとても大事な式になります。

得られた式で問題を解く。まずは要素数の式で。

それでは、元の問題に戻って問題を解いてみましょう。

「３より大きいことがわかっている (A)」ときの「偶数である (B)」確率 \(P(B|A)\) です。

要素数の式は次の通りです。

つまり、A の要素数 n(A) と、A と B の重なりの部分の数から計算します。

この図から \(n(A) = 3\) で、重なりの部分の要素数は \(n(A\cap B)= 2\) です。したがって、

\[ P(B | A) = \frac{n(A \cap B)}{n(A)} = \frac{2}{3} \approx 0.67 \]

となり、答えがわかりました。

得られた式で問題を解く。次は確率の式で。

条件付き確率 \(P(B|A)\) を確率で表した次の式を使って問題を解いてみます。

この問題では \(P(A)\) や \(P(A \cap B)\) は与えられていないので、それぞれ計算する必要があります。

まず \(P(A)\) は全体の要素数 \(n(U)\) に対する A の要素数 \(n(A)\) とから、次のように求められます。

\[ P(A) = \frac{n(A)}{n(U)} = \frac{3}{6} = \frac{1}{2} \]

\(P(A \cap B)\) は全体の要素数 \(n(U)\) に対する A ∩ B の要素数 \(n(A \cap B)\) とから、次のように求められます。

\[ P(A\cap B) = \frac{n(A \cap B)}{n(U)} = \frac{2}{6} = \frac{1}{3} \]

したがって条件付き確率 \(P(B|A)\) は

\[ P(B | A) = \frac{P(A \cap B)}{P(A)} = \frac{1/3}{1/2} = \frac{2}{3} \approx 0.67 \]

この方法でも、確かに正しい答えが得られました。

以上、条件付き確率の基本的な考え方について説明しました。