面積素とパラメータ

曲面 $S$ 上の位置ベクトルを $u, v$ をパラメータとして、次のように表します。

$$\overrightarrow{r}(u,v) = x(u,v) \overrightarrow{i} + y(u,v) \overrightarrow{j} + z(u,v) \overrightarrow{k}$$

さて、このときパラメータ $u$ と $v$ が微小変化したときに、曲面 $S$ 上の対応する点がどのくらい動くか考えます。 そして、この微小変化がなす面積が、$uv$ 平面と曲面 $S$ とで、どのくらい変わるかみてみましょう。

まず、$uv$ 平面を考えます。$u$ が $\Delta u$ だけ変化し、$v$ が $\Delta v$ だけ変化したとします。 このとき、この微小量がなす面積 $\Delta A$ は $\Delta u \Delta v$ です。

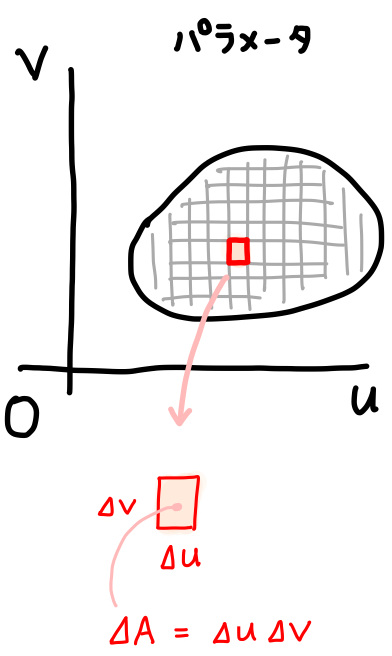
ちなみに面を微小区画に分けたひとつひとつを面積素といいます。面積素 $\Delta A$ の面積は $\Delta u \Delta v$ です。

これに対して、曲面 $S$ でどうなるでしょうか。

まず、スタート地点としてパラメータ $(u, v)$ に対して、点 $P$ を対応付けて、その位置ベクトルを $\overrightarrow{r}(u,v)$ とします。

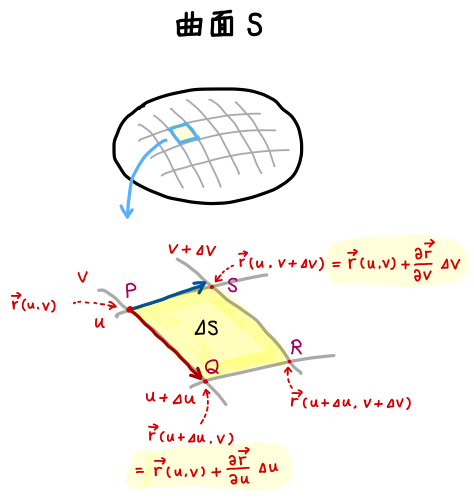
$u$ が $\Delta u$ だけ微小増加した点 $Q$ の位置ベクトルは、$\overrightarrow{r}(u+\Delta u, v)$ です。 高次の微小量を無視すると、$\overrightarrow{r}(u+\Delta u, v)$ は次のようにかけます。

$$\overrightarrow{r}(u+\Delta u, v) = \overrightarrow{r}(u,v) + \frac{\partial \overrightarrow{r}}{\partial u} \Delta u$$

従って、ベクトル $\overrightarrow{PQ}$ は次となります。

$$\begin{aligned} \overrightarrow{PQ} &= \overrightarrow{r}(u+\Delta u, v) - \overrightarrow{r}(u,v)\\ &= \frac{\partial \overrightarrow{r}}{\partial u} \Delta u \end{aligned}$$

同様に $v$ の微小変化を考えると、

$$\overrightarrow{r}(u, v+\Delta v) = \overrightarrow{r}(u,v) + \frac{\partial \overrightarrow{r}}{\partial v} \Delta v$$

ですから、

$$\begin{aligned} \overrightarrow{PS} &= \overrightarrow{r}(u, v+\Delta v) - \overrightarrow{r}(u,v)\\ &= \frac{\partial \overrightarrow{r}}{\partial v} \Delta v \end{aligned}$$

となります。

一般に２つのベクトル $\overrightarrow{a}$ と $\overrightarrow{b}$ が作る平行四辺形の面積は、$| \overrightarrow{a} \times \overrightarrow{b}|$ で求められます。

従って、平行四辺形 $PQRS$ の面積 $\Delta S$ は $| \overrightarrow{PQ} \times \overrightarrow{PS} |$ です。 上の結果から、面積素 $\Delta S$ の大きさ (面積) は次のように書けます。

$$\begin{aligned} \Delta S &= | \overrightarrow{PQ} \times \overrightarrow{PS} | \\ &= \Big| \frac{\partial \overrightarrow{r}}{\partial u} \Delta u \times \frac{\partial \overrightarrow{r}}{\partial v} \Delta v \Big| \\ &= \Big| \frac{\partial \overrightarrow{r}}{\partial u} \times \frac{\partial \overrightarrow{r}}{\partial v} \Big| \Delta u \Delta v \\ &= \Big| \frac{\partial \overrightarrow{r}}{\partial u} \times \frac{\partial \overrightarrow{r}}{\partial v} \Big| \Delta A \\ \end{aligned}$$

この式が $uv$ 平面の面積素 $\Delta A$ と、パラメータの変化に対応した曲面上の面積素 $\Delta S$ の関係式になります。