グラム・シュミットの正規直交化法

グラム・シュミットの正規直交化法とは？

ある内積空間 \(V^n\) のひと組の基底を \(\{ \overrightarrow{u_1}, \overrightarrow{u_2}, \cdots, \overrightarrow{u_n} \}\) とします。

このとき、 \(\overrightarrow{v_1} = \overrightarrow{u_1}\) とし、 \(2 \le k \le n\) で \(\overrightarrow{v_k}\) を次のようにとります。

すると、\(\{ \overrightarrow{v_1}, \overrightarrow{v_2}, \cdots, \overrightarrow{v_n} \}\) は \(V^n\) の直交基底となります。

さらに、 \(1 \le k \le n\) で \(\overrightarrow{e_k} = \cfrac{ \overrightarrow{v_k} }{ \| \overrightarrow{v_k} \| } \) としたときの \(\{ \overrightarrow{e_1}, \overrightarrow{e_2}, \cdots, \overrightarrow{e_n} \}\) は \(V^n\) の正規直交基底となります。

こうした方法で、ある基底から正規直交基底を作る方法を グラム・シュミットの正規直交化法 (Gram-Schmidt Orthogonalization) と言います。

グラム・シュミットの正規直交化法の仕組み

それではなぜ、上の方法で正規直交基底が求められるのか、\(n=3\) までの状況を図で確認しておきましょう。

まず最初に \(\overrightarrow{v_1} = \overrightarrow{u_1}\) とします。

次に下図のような関係として \(\overrightarrow{v_2}\) をとることを考えます。

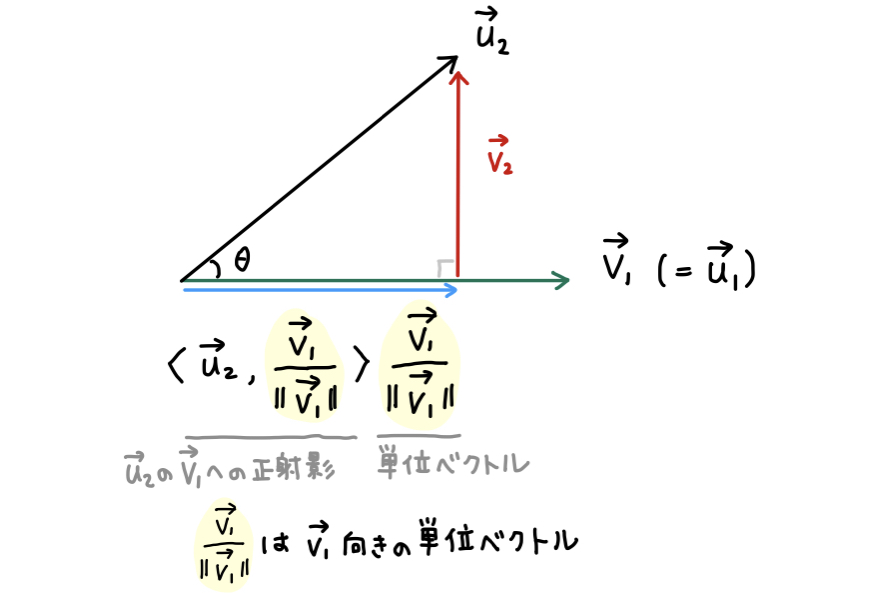
\(\overrightarrow{u_2}\) の \(\overrightarrow{v_1}\) 上への正射影の大きさは、 \(\overrightarrow{u_2}\) と \(\overrightarrow{v_1}\) 向きの単位ベクトルとの内積で求まります。 \(\overrightarrow{v_1}\) 向きの単位ベクトルは、自身の大きさで割った \(\cfrac{\overrightarrow{v_1}}{\| \overrightarrow{v_1} \| }\) です。

したがって、\(\overrightarrow{u_2}\) の \(\overrightarrow{v_1}\) 上への正射影の大きさは

\[ \Big\langle \overrightarrow{u_2}, \cfrac{\overrightarrow{v_1}}{\| \overrightarrow{v_1} \|} \Big\rangle \]

となります。

よって、図の水色のベクトル (つまり、大きさが「\(\overrightarrow{u_2}\) の \(\overrightarrow{v_1}\) 上への正射影」の大きさで、向きが \(\overrightarrow{v_1}\) 向きのベクトル) は、 次の式で求められます。

\[ \begin{aligned} \Big\langle \overrightarrow{u_2}, \cfrac{\overrightarrow{v_1}}{\| \overrightarrow{v_1} \|} \Big\rangle \cfrac{\overrightarrow{v_1}}{\| \overrightarrow{v_1} \|} &= \langle \overrightarrow{u_2}, \overrightarrow{v_1} \rangle \cfrac{\overrightarrow{v_1}}{\| \overrightarrow{v_1} \|^2} \\ &= \cfrac{\langle \overrightarrow{u_2}, \overrightarrow{v_1} \rangle}{\langle \overrightarrow{v_1}, \overrightarrow{v_1} \rangle} \overrightarrow{v_1} \end{aligned} \]

よって、\(\overrightarrow{v_2}\) は図から明らかに次の式であることがわかります。

\[ \overrightarrow{v_2} = \overrightarrow{u_2} - \cfrac{\langle \overrightarrow{u_2}, \overrightarrow{v_1} \rangle}{\langle \overrightarrow{v_1}, \overrightarrow{v_1} \rangle} \overrightarrow{v_1} \]

これで直交する \(\overrightarrow{v_1}\) と \(\overrightarrow{v_2}\) が求まりました。次に \(\overrightarrow{v_3}\) を考えましょう。

\(\overrightarrow{v_3}\) は下の図のようにとるようにしましょう。\(xyz\) の直交座標系のようにみれば \(x\)軸、\(y\)軸、\(z\)軸をそれぞれ \(\overrightarrow{v_1}\)、\(\overrightarrow{v_2}\)、\(\overrightarrow{v_3}\) 向きにとったような形になっています。

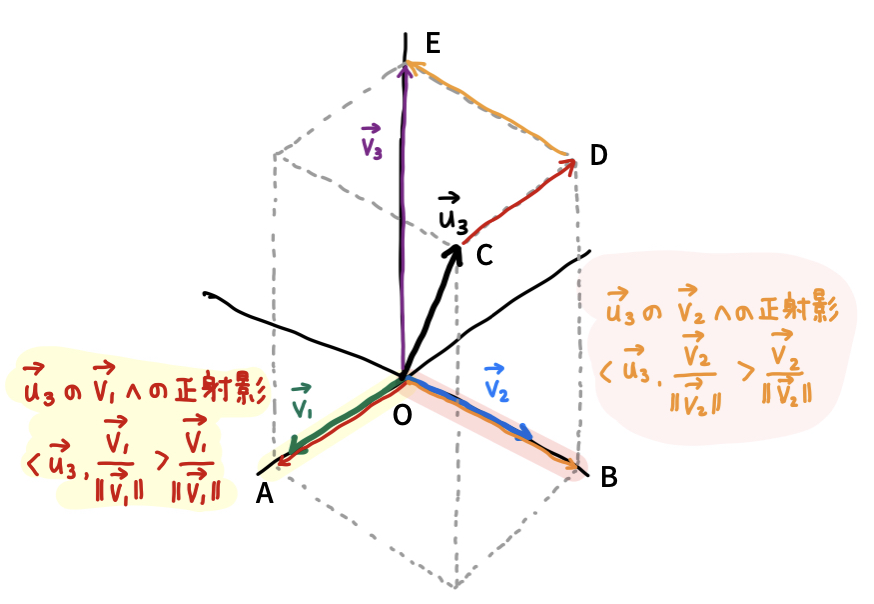
すると上と同様に、\(\overrightarrow{u_3}\) の \(\overrightarrow{v_1}\) 上への正射影の大きさは \(\Big\langle \overrightarrow{u_3}, \cfrac{\overrightarrow{v_1}}{\|\overrightarrow{v_1}\|}\Big\rangle \)、 \(\overrightarrow{u_3}\) の \(\overrightarrow{v_2}\) 上への正射影の大きさは \(\Big\langle \overrightarrow{u_3}, \cfrac{\overrightarrow{v_2}}{\|\overrightarrow{v_2}\|}\Big\rangle \) です。

よって、図内の点 O, A, B, C, D, E を取ると、それぞれ次であることがわかります。

\[ \begin{aligned} \overrightarrow{OA} &= \Big\langle \overrightarrow{u_3}, \cfrac{\overrightarrow{v_1}}{\|\overrightarrow{v_1}\|}\Big\rangle \cfrac{\overrightarrow{v_1}}{\|\overrightarrow{v_1}\|} \\ \overrightarrow{OB} &= \Big\langle \overrightarrow{u_3}, \cfrac{\overrightarrow{v_2}}{\|\overrightarrow{v_2}\|}\Big\rangle \cfrac{\overrightarrow{v_2}}{\|\overrightarrow{v_2}\|} \\ \overrightarrow{CD} &= - \overrightarrow{OA} \\ \overrightarrow{DE} &= - \overrightarrow{OB} \end{aligned} \]

以上から、\(\overrightarrow{v_3}\) は次のように求まります。

\[ \begin{aligned} \overrightarrow{v_3} &= \overrightarrow{OE} \\ &= \overrightarrow{OC} + \overrightarrow{CD} + \overrightarrow{DE} \\ &= \overrightarrow{u_3} - \overrightarrow{OA} - \overrightarrow{OB} \\ &= \overrightarrow{u_3} - \Big\langle \overrightarrow{u_3}, \cfrac{\overrightarrow{v_1}}{\|\overrightarrow{v_1}\|}\Big\rangle \cfrac{\overrightarrow{v_1}}{\|\overrightarrow{v_1}\|} - \Big\langle \overrightarrow{u_3}, \cfrac{\overrightarrow{v_2}}{\|\overrightarrow{v_2}\|}\Big\rangle \cfrac{\overrightarrow{v_2}}{\|\overrightarrow{v_2}\|} \\ &= \overrightarrow{u_3} - \cfrac{\langle \overrightarrow{u_3}, \overrightarrow{v_1} \rangle}{\langle \overrightarrow{v_1}, \overrightarrow{v_1} \rangle} \overrightarrow{v_1} - \cfrac{\langle \overrightarrow{u_3}, \overrightarrow{v_2} \rangle}{\langle \overrightarrow{v_2}, \overrightarrow{v_2} \rangle} \overrightarrow{v_2} \end{aligned} \]

これで直交基底 \(\overrightarrow{v_2}\)、\(\overrightarrow{v_3}\) が求められました。これらは上の \((A)\) で \(k=2, 3\) とした場合と一致しています。

また \(\overrightarrow{v_k}\) を正規化する (つまり大きさ1のベクトルにする) には、単に自身の大きさで割れば良いので、正規直交系 \(\{ \overrightarrow{e_1}, \overrightarrow{e_2}, \cdots, \overrightarrow{e_n} \}\) は \(\{ \cfrac{\overrightarrow{v_1}}{\|\overrightarrow{v_1}\|}, \cfrac{\overrightarrow{v_2}}{\|\overrightarrow{v_2}\|}, \cdots, \cfrac{\overrightarrow{v_n}}{\|\overrightarrow{v_n}\|}\}\) となる、というわけです。