正弦定理

正弦定理は三角形の内角の正弦とその対辺との関係を示したものです。

次の三角形 ABC の内角を \(A\), \(B\), \(C\) として、それぞれの対辺を \(a\)、\(b\)、\(c\) とします。

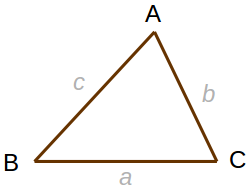
この時に次の関係が成り立つことを正弦定理といいます。

\[ \frac{a}{\sin A} = \frac{b}{\sin B} = \frac{c}{\sin C} = 2R \]

\(R\) は外接円の半径です。

英語では The law of sines。law は法則で、定理なら theorem です。しかし通常、正弦「法則」というより、正弦「定理」という方が一般的と思うのでそのままにします。

内角 \(A\) が \(0 \lt \angle A \lt 90\degree\) のときは、外接円の中心を通る \(BD\) を考えると、円周角の定理から \(\angle A = \angle D\) となります。

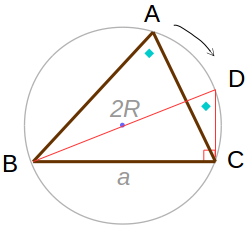
\(BD\) が外接円の中心を通るのでタレスの定理より、\(\angle C = 90\degree\) となります。

上図の赤三角形から、次の関係がわかります。

\[ \begin{aligned} 2R \sin D &= a \\ \therefore 2R &= \frac{a}{\sin D} = \frac{a}{\sin A} \end{aligned} \]

\(\angle A = 90\degree\) の場合を考えます。

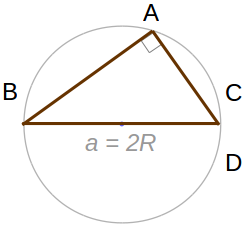
\(\sin A = \sin 90\degree = 1\) と \(a = 2R\) であることから、直ちに次がわかります。

\[ \begin{aligned} a &= 2R \\ \frac{a}{\sin A} &= 2R \end{aligned} \]

\(90\degree \lt \angle A \lt 180\degree\) の場合は、外接円の中心を通る \(BD\) を考えます。

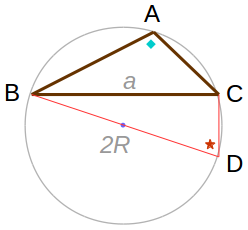
出来上がった四角形 \(ABDC\) で、円に内接する四角形の対辺の和は \(180\degree\) なので、 \(\angle A + \angle D = 180\degree\) です。

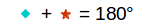
\(\angle BCD = 90\degree\) ですから、次が分かります。

\[ \begin{aligned} 2R \sin D &= a \\ \therefore 2R &= \frac{a}{\sin D} = \frac{a}{\sin A} \end{aligned} \]

ここで \(\sin D = \sin (180\degree - A) = \sin A \) であることを使いました。