転置行列
転置行列とは
任意の\((m,n)\)行列 \(A = [a_{ij}]\) に対して、行と列を入れ替えた行列 \([a_{ji}]\) を、 行列 \(A\) の転置行列 (transpose of A) といいます。
行列 \(A\) の転置行列は、\({}^{t}A\) と表記したり、\(A^{T}\) と表記したりします。
日本の教科書では主に \({}^{t}A\) と表記することが多く、アメリカの教科書では \(A^{T}\) と表記するのが普通のようです。 このサイトでは、当方がアメリカ在住なので、\(A^{T}\) と書くことにします。
具体例としては、
\[ A = \begin{bmatrix} 1 & 2 & 3\\ 4 & 5 & 6 \end{bmatrix} \]
のとき、\(A\) の転置行列は
\[ A^{T} = \begin{bmatrix} 1 & 4\\ 2 & 5\\ 3 & 6 \end{bmatrix} \]
になります。行と列を入れ替えるだけです。例えば、\(A\) の\(1\)行\(2\)列目の成分の値\(2\)は、その転置行列の\(2\)行\(1\)列目の成分になっています。
転置行列の性質
転置行列の性質をみていきましょう。
\[ (A^{T})^{T} = A \]
行列 \(A\) を転置して、もう一度転置すると、\(A\) に戻るということです。
当たり前といってはあれなので、一応書くと、\(A = [a_{ij}]\) なら \(A^T = [a_{ji}]\) です。もう一度転置すれば \((A^T)^T = [a_{ij}]\)。したがって、\((A^T)^T = A\) です。
\[ (A+B)^{T} = A^T + B^T \]
\(A = [a_{ij}]\)、\(B = [b_{ij}]\) とすると、\(A^T = [a_{ji}]\)、\(B^T = [b_{ji}]\)、\(A+B = [a_{ij} + b_{ij}]\) です。したがって、\((A+B)^T = [a_{ji} + b_{ji}] = [a_{ji}] + [b_{ji}] = A^T + B^T\)。
\[(AB)^T = B^T A^T\]
積が定義されるように、行列のサイズを行列 \(A\) は \((p,q)\)行列、\(B\)は \((q,r)\) 行列とします。
\(AB = [c_{ij}]\) とすると、積 \(AB\) の \(ij\) 成分 (\(i\)行\(j\)列目成分) は、次の図のハイライトした箇所の積和 (成分毎かけて足していく) ですから
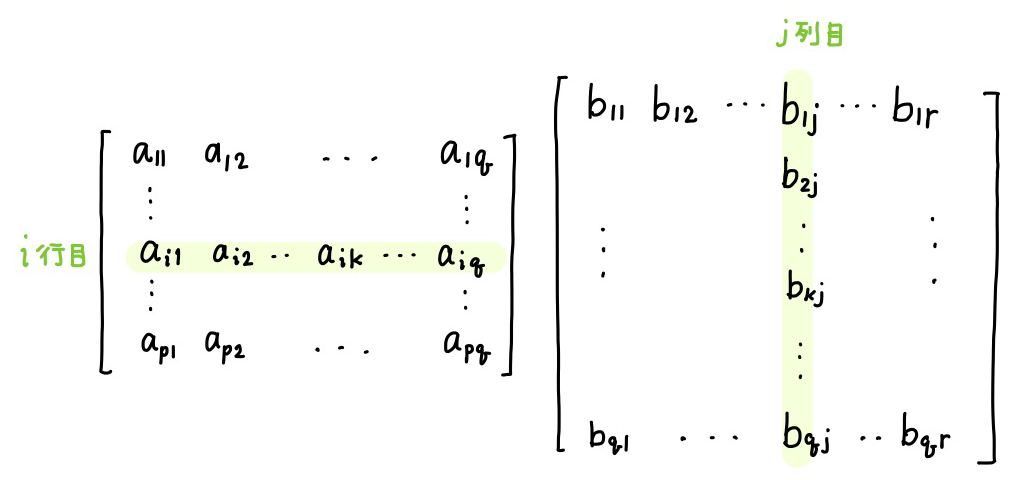
\[c_{ij} = \sum_{k=1}^{q} a_{ik} b_{kj}\]
となります。
ですから、これの転置は \(i\) と \(j\) を入れ替えて
\[(AB)^T = [c_{ji}] = \Big[ \sum_{k=1}^{q} a_{jk} b_{ki} \Big] \tag{1}\]
となります。
一方、\(B^T A^T = [d_{ij}]\) とすると、\(B^T\) と \(A^T\) の積は、次の図のハイライトした箇所の積和ですから
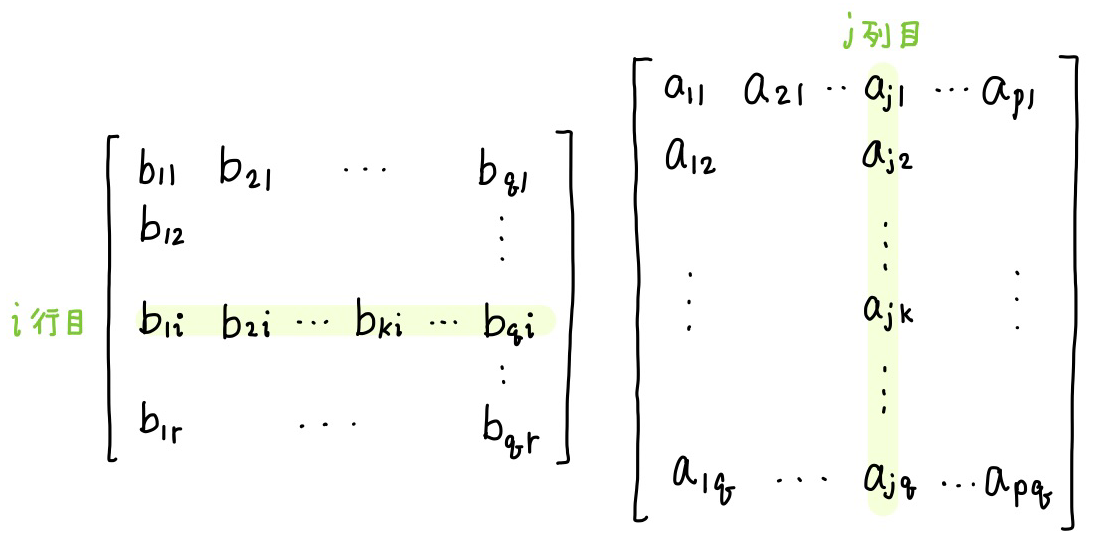
\[d_{ij} = \sum_{k=1}^q b_{ki} a_{jk}\]
となります。つまり、
\[B^T A^T = \Big[\sum_{k=1}^q b_{ki} a_{jk}\Big] \tag{2}\]
です。\(a_{jk} b_{ki} = b_{ki} a_{jk}\) ですから、\((1)\) と \((2)\) から
\[ (AB)^T = B^T A^T\]
であることがわかります。