ストークスの定理
\(\overrightarrow{F}(x,y,z)\) のベクトル場において、閉曲線 \(C\) を境界とする向きのついた曲面を \(S\) とする。 \(\overrightarrow{F}\) が \(S\) 上で連続な偏導関数をもち、\(C\) を含めて連続とする。このとき次の関係がなりたち、これをストークスの定理という。
\[
\int_S (\nabla \times \overrightarrow{F}) \cdot \overrightarrow{n} dS = \int_C \overrightarrow{F} \cdot d\overrightarrow{r}
\]
ここで \(\overrightarrow{n}\) は \(S\) の単位法線ベクトルであり、曲線 \(C\) の向きは曲面の正の側から見て反時計周りの方向とする。
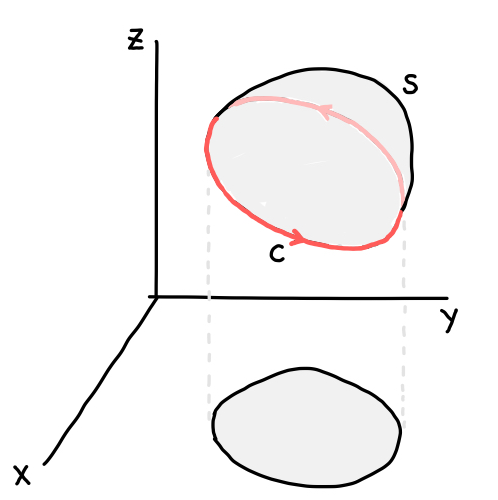
この式はつまり、「\(\overrightarrow{F}\) の回転 (\(\text{rot}\overrightarrow{F}\))の \(S\) 上での法線面積分は、\(\overrightarrow{F}\) の \(C\) における接線線積分に等しい」ということを表しています。