ヘビサイドの階段関数
ヘビサイドの階段関数とは
ヘビサイドの階段関数 (Heaviside step function) (または ヘビサイド関数、単位階段関数 とも呼ばれます) は、ランプ関数の導関数として定義できます。
\[
H(x) = \frac{d}{dx} R(x)
\]
ここで、ランプ関数 (Ramp function) は 1 変数の実数値関数で \(x\) を実数として次のように定義されます。
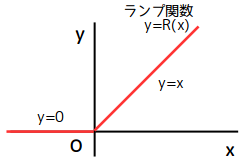
\[
R(x) = \begin{cases}
\ x &( x \ge 0 )\\
\ 0 &( x \lt 0 )
\end{cases}
\]
グラフからわかるように、ランプ関数の接線の傾き (微分係数) は \(x \lt 0\) では \(0\)、\(x \gt 0\) で \(1\) となります。 したがって、ヘビサイドの階段関数のとる値は
\[
H(x) = \begin{cases}
\ 1 &( x \gt 0 )\\
\ 0 &( x \lt 0 )
\end{cases}
\]
となります。\(R(x)\) は \(x=0\) で微分可能ではないので、\(H(x)\) は \(x=0\) で未定義です。
ヘビサイド関数と物理量
変数を時刻 \(t\) として考えると、ヘビサイド関数はある時刻 \(t=a\) まで 0 (OFF) だったものが、\(t=a\) を境に 1 (ON) となる関数といえます。ラプラス変換で用いられる場合は、この状況を次のように書く場合が多いです。
\[
u (t-a) = \begin{cases}
0 &( t \lt a ) \\
1 &( t \gt a )
\end{cases}
\]
これを使うと、ある物理量 \(f(t)\) がある時刻 \(t=a\) で入力される (ON となる) 場合は、\(f(t)u(t-a)\) と書くことができます。
ヘビサイド関数を使ってマスクされたような形のラプラス変換に関しては、「ラプラス変換の第二移動法則」で扱っています。