点と平面の距離

ある平面 \(ax+by+cz+d=0\) と点P \((x_0, y_0, z_0)\) との距離 \(D\) は、次の式で求められます。

\[ D = \frac{|ax_0+by_0+cz_0+d|}{\sqrt{a^2+b^2+c^2}} \]

距離は英語で Distance です。そのためここで記号は D を使っています。

なぜこれで平面と点との距離が求められるのか、考えてみましょう。

点 P から平面に下ろした垂線の足を点 R とします。平面と点P \((x_0,y_0,z_0)\) との距離 \(D\) というのは、PR の長さ \(\overline{PR}\) のことです。

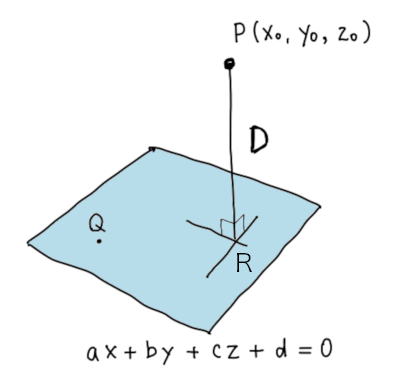
さて、平面上の任意の点Q \((x_1,y_1,z_1)\) を考えると、点\(P\)、点\(Q\)、点\(R\) の3点を通る平面は次の図のようになります。

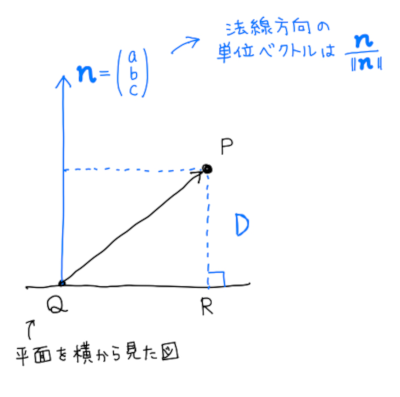
この関係から、\(\overline{PR}\) はベクトル \(\overrightarrow{QP}\) の法線方向の成分の大きさであることがわかります。

ここで「成分」と言わずわざわざ「成分の大きさ」と言っているのは、例えば座標の関係から法線方向の成分がマイナスとなる場合もあるからです。この場合はその成分の絶対値 (大きさ) が距離を表します。

ここで少しおさらいをしておきます。

一般に、あるベクトル \(\overrightarrow{A}\) のベクトル \(\overrightarrow{B}\) 向きの成分を取り出すには、「ベクトル \(\overrightarrow{B}\) 向きの単位ベクトル」と \(\overrightarrow{A}\) との内積を計算することによって求められます。

「ベクトル \(\overrightarrow{B}\) 向きの単位ベクトル」というのは、\(\overrightarrow{B}\) を \(\overrightarrow{B}\) 自身の大きさ \(\|\overrightarrow{B}\|\) で割れば単位ベクトルになります。（例えば、大きさ \(10\) のベクトルは大きさを \(10\) で割れば大きさ \(1\) のベクトル（すなわち単位ベクトル）になりますよね）

さて、平面 \(ax+by+cz+d=0\) の法線ベクトルを \(\overrightarrow{n}\) とすると、法線向きの単位ベクトルは \(\displaystyle\frac{\overrightarrow{n}}{\|\overrightarrow{n}\|}\) です。

平面の法線ベクトルについては、「平面と法線ベクトル」をみてください。

よって、\(\overrightarrow{QP}\) の法線方向の成分の大きさ \(\overline{PR}\) は、次の式で求められます。

\[ \begin{aligned} \overline{PR} &= \Big| \overrightarrow{QP} \bold{\cdot} \frac{\overrightarrow{n}}{\|\overrightarrow{n}\|} \Big| \\ &= \frac{| \overrightarrow{QP} \bold{\cdot} \overrightarrow{n}|}{\|\overrightarrow{n}\|} \end{aligned} \]

これが点P と平面との距離になっています。

これだけでは計算できないので、この式をもっとしっかり整理していきましょう。

まず、ベクトル \(\overrightarrow{QP}\) は点P \((x_0,y_0,z_0)\)、点Q \((x_1,y_1,z_1)\) という座標から、その成分は直ちに次のようにかけます。

\[ \overrightarrow{QP} = \langle x_0-x_1, y_0-y_1, z_0-z_1 \rangle \]

また法線ベクトル \(\overrightarrow{n}\) の成分は \(\overrightarrow{n} = \langle a,b,c \rangle\) です。またその大きさ \(\|\overrightarrow{n}\|\) は \(\|\overrightarrow{n}\| = \sqrt{a^2+b^2+c^2}\) です。したがって、

\[ \frac{\overrightarrow{n}}{\|\overrightarrow{n}\|} = \frac{1}{\sqrt{a^2+b^2+c^2}} \langle a, b, c \rangle \]

以上から、\(D\) は次のようになります。

\[ \begin{aligned} D &= \overline{PR}\\ &= \frac{| \overrightarrow{QP} \bold{\cdot} \overrightarrow{n}|}{\|\overrightarrow{n}\|} \\ &= \frac{| \langle x_0-x_1, y_0-y_1, z_0-z_1 \rangle \cdot \langle a,b,c \rangle |}{\sqrt{a^2+b^2+c^2}} \\ &= \frac{|a(x_0-x_1)+b(y_0-y_1)+c(z_0-z_1)|}{\sqrt{a^2+b^2+c^2}} \end{aligned} \]

ここで、分子の絶対値記号の中を整理しましょう。

点Q \((x_1,y_1,z_1)\) は与えられた平面上にあるので、平面の方程式を満たします。つまり、\(ax_1+by_1+cz_1+d=0\)、すなわち \(ax_1+by_1+cz_1 = -d\) です。

これを踏まえると、

\[ \begin{aligned} a(x_0-x_1)+b(y_0-y_1)+c(z_0-z_1) &= ax_0 + by_0 + cz_0 - (ax_1 + by_1 + cz_1)\\ &= ax_0 + by_0 + cz_0 + d \end{aligned} \]

以上から、平面 \(ax+by+cz+d=0\) と点\((x_0,y_0,z_0)\) との距離は次の式でもとまることがわかりました。

\[ \begin{aligned} D &= \frac{|ax_0 + by_0 + cz_0 + d|}{\sqrt{a^2+b^2+c^2}} \end{aligned} \]