ベクトルの線積分

\(\overrightarrow{F} = F_1(x,y,z) \overrightarrow{i} + F_2(x,y,z) \overrightarrow{j} + F_3(x,y,z) \overrightarrow{k}\) のベクトル空間内の \(2\)点 \(A\) から \(B\) を結ぶ曲線経路 \(C\) があります。

この曲線上で、ベクトル \(\overrightarrow{F}\) の接線方向成分の大きさを表すスカラー関数 \(F_t(s) \) を考えます。\(s\) は \(A\) からの孤の長さです。

\(F_t(s)\) の線積分は次の式になります。

\[\int_C F_t ds\]

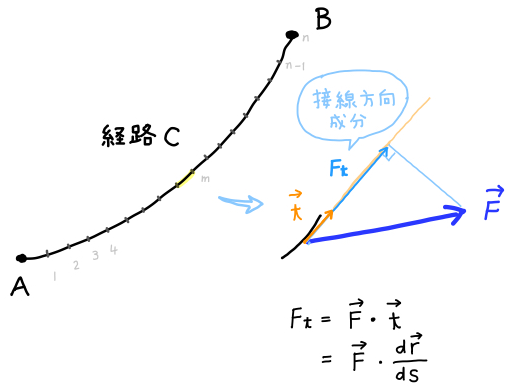
ここで\(F_t(s)\) は \(C\)の単位接線ベクトル \(\overrightarrow{t}(s)\) とベクトル \(\overrightarrow{F}\) の内積として求まりますので、次のように書けます。

\[ \int_C F_t ds = \int_C \overrightarrow{F} \cdot \overrightarrow{t} ds \]

この量をベクトル \(\overrightarrow{F}\) の線積分 (接線線積分) といいます。

曲線 \(C\) を \(s\) をパラメータとして、\(\overrightarrow{r}(s) = x(s)\overrightarrow{i} + y(s)\overrightarrow{j} + z(s)\overrightarrow{k}\) と表すと、 単位接線ベクトル \(\overrightarrow{t}\) は \(\overrightarrow{t} = \displaystyle\frac{d\overrightarrow{r}}{ds}\) です。

よって、ベクトル \(\overrightarrow{F}\) の線積分は次のようにも書けます。

\[ \begin{aligned} \int_C \overrightarrow{F} \cdot \overrightarrow{t} ds &= \int_C \overrightarrow{F} \cdot \frac{d\overrightarrow{r}}{ds} ds\\ &= \int_C \overrightarrow{F} \cdot d\overrightarrow{r} \end{aligned} \]

以上、書き方が色々あって戸惑ってしまうかもしれませんが、ポイントは経路 \(C\) でベクトル場の接線成分を積分する、という点です。

それでは、いくつか実際に問題を解きながら、ベクトルの線積分に関する理解を深めましょう。

• ベクトルの線積分 例題 (1)
• ベクトルの線積分 例題 (2)