等位面とは?
スカラー関数 \(f(x,y,z)\) に対して、\(f(x,y,z)=c\) (\(c\) は定数) を満たす点 \((x,y,z)\) の集合はひとつの曲面を表し、これを等位面という。
これはいったい、どういうことでしょうか?
等位面をイメージするために、部屋の温度分布を考えてみましょう。
例えば、部屋の中に暖房がひとつあるとします。すると、室温は暖房側が一番暖かく、遠ざかるにつれて寒くなるでしょう。 (風の流れとかいろんな要素で室温は変わると思いますが、単純化して考えてください)
部屋を上から見て、温度の分布を線で書くと次のようになるでしょう。
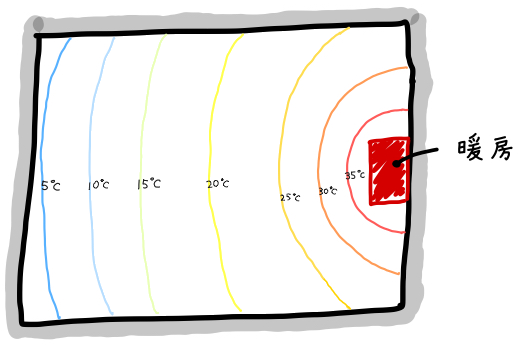
この温度分布を場所 \((x,y,z)\) の関数 \(T\) で表します。
そして、室温が摂氏25度である場所を \(T(x,y,z) = 25\) と書きましょう。 26度の場所は \(T(x,y,z)=26\)、27度の場所は \(T(x,y,z)=27\)・・・ です。
真上からみた上の図では温度分布は「線」として書かれていましたが、高さがあるので、同じ温度の部分は「面」になります。
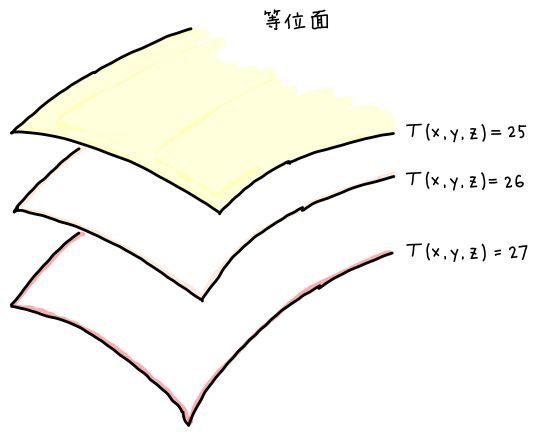
この面のように、関数として同じ値をとる「面」を等位面 (equipotential surface) といいます。
この等位面の性質として、ある点 \((x,y,z)\) の値 (上の例では室温) はただ1つに決まるので、複数の等位面は交わることはありません。