線積分
\(xy\) 平面上に経路 \(C\) と、 \(C\) 上での 2 変数のスカラー関数 \(f(x,y)\) を考えます。 \(f(x,y)\) が \(C\) 上に作るカーテンの面積を計算しましょう。
このために経路 \(C\) を \(n\) 個にコマ切れに分割します。
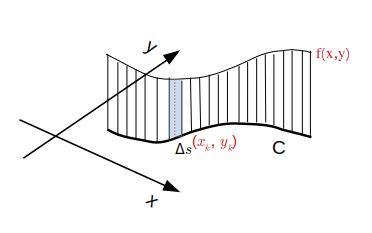
コマ切れに分割した \(k\) 番目の線素 \(\Delta s_k\) とその線素内の座標 \((x_k,y_k)\) での関数値 \(f(x_k, y_k)\) の積は、 カーテンを短冊状に切った一片の面積になります。したがって、カーテン全体の面積 \(A\) は分割数 \(n\) を無限に大きくしたときの短冊の面積の総和として求められます。
\[ A = \lim_{n \to \infty} \sum_{k=1}^n f(x_k, y_k) \Delta s_k = \int_C f(x, y) ds \]
これを曲線 \(C\) に沿った線積分 (line integral) といいます。 この場合曲線 \(C\) のことを積分経路といいます。
\(x\) と \(y\) をパラメータ表示する場合
曲線を表す場合、\(x\) と \(y\) をパラメータを使って表示すると見通しが良くなることが多いです。 例えば考える曲線が円なら、\(\theta\) をパラメータとして \(x = \cos \theta\)、\(y = \sin \theta\) とすると良かったりします。
そこで、\(x\) と \(y\) が \(t\) をパラメータとして \(x = x(t)\)、\(y=y(t)\) と表されるときに、線積分がどうなるかみておきます。
線素 \(ds\) は図から次のように求められます。
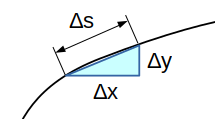
\[ \begin{aligned} ds &= \lim_{\Delta \to 0} \Delta s\\ &= \lim_{\Delta \to 0} \sqrt{ (\Delta x)^2 + (\Delta y)^2} \\ &= \lim_{\Delta \to 0} \sqrt{ \Big(\frac{\Delta x}{\Delta t}\Big)^2 + \Big(\frac{\Delta y}{\Delta t}\Big)^2} \Delta t\\ &= \sqrt{ \Big(\frac{dx}{dt}\Big)^2 + \Big(\frac{dy}{dt}\Big)^2} dt \end{aligned} \]
「弧長を求める」も参考にしてください。同様のことをしてます。
よって、上の線積分はパラメータ \(t\) を用いて次のように書けます。
\[ \int_C f(x, y) ds = \int_C f(x(t), y(t)) \sqrt{ \Big(\frac{dx}{dt}\Big)^2 + \Big(\frac{dy}{dt}\Big)^2} dt \]
また \(x\) 軸に沿う線積分、\(y\) 軸に沿う線積分は、線素 \(ds\) はそれぞれ \(dx\)、\(dy\) になるので次のように書けます。
\[ \begin{aligned} \int_C f(x, y) dx &= \int_C f(x(t), y(t)) x'(t) dt \\ \int_C g(x, y) dy &= \int_C g(x(t), y(t)) y'(t) dt \end{aligned} \]
\(x\) 軸方向の変位、\(y\) 軸方向の変位が同時に起こる場合は、次のようにまとめてかけます。
\[ \begin{aligned} \int_C f(x, y) dx + g(x,y) dy \end{aligned} \]
見慣れない形をしていますが、積分経路 \(C\) が共通なので \(\int_C\) が省略されているだけで、次の式と同じです。
\[ \begin{aligned} \int_C f(x, y) dx + g(x,y) dy = \int_C f(x, y) dx + \int_C g(x, y) dy \end{aligned} \]