流線
あるベクトル場 \(\overrightarrow{F}=F_1\overrightarrow{i}+F_2\overrightarrow{j}+F_3\overrightarrow{k}\) である曲線 \(C\) があり、\(C\) 上の各点 \(P\) におけるベクトル \(\overrightarrow{F}(P)\) が 曲線 \(C\) に接している時、この曲線 \(C\) をベクトル場 \(\overrightarrow{F}\) の流線といいます。
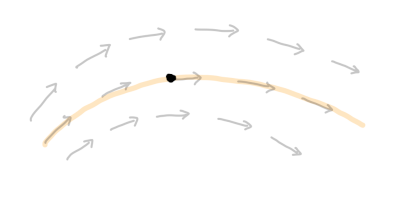
ここで一般に \(F_1\)、 \(F_2\)、\(F_3\) は座標 \((x,y,z)\) の関数で、細かくかけば \(\overrightarrow{F}=F_1(x,y,z)\overrightarrow{i}+F_2(x,y,z)\overrightarrow{j}+F_3(x,y,z)\overrightarrow{k}\) というところですが、簡単に上のように書いてます。
さてこの時、流線の方程式は次の微分方程式を解くことで求められることになってます。
\[
\frac{dx}{F_1} = \frac{dy}{F_2} = \frac{dz}{F_3}
\]
さっそく例題を考えてみましょう。