ベクトルの内積

ベクトル $\overrightarrow{a}$ とベクトル $\overrightarrow{b}$ の内積 (ドット積) $\overrightarrow{a} \cdot \overrightarrow{b}$ の書き方について説明します。

簡単にするため 2 次元のベクトルで考えます。 $\overrightarrow{a}$ とベクトル $\overrightarrow{b}$ の成分をそれぞれ、 $\overrightarrow{a} = \langle a_1, a_2 \rangle$ 及び $\overrightarrow{b} = \langle b_1, b_2 \rangle$ とします。

座標と区別して、ベクトルの成分であることを示すのに、 $\langle$ と $\rangle$ で囲んで書きます。

$x$ 、 $y$ 、 $z$ 軸方向の基本ベクトルをそれぞれ $\overrightarrow{i}$ 、 $\overrightarrow{j}$ 、 $\overrightarrow{k}$ とすれば、 $\overrightarrow{a} = \langle a_1, a_2, a_3 \rangle$ は $\overrightarrow{a} = a_1 \overrightarrow{i} + a_2 \overrightarrow{j} + a_3 \overrightarrow{k}$ のことです。

表記について

ベクトルの成分表示に $\langle$ と $\rangle$ を使うのは、アメリカの数学の教科書で一般的なので、このサイトでもそれを採用しています。しかし、別にアメリカ方式が正しいとか、これがおすすめなどと言うつもりは全くありません。ただ当方がアメリカ在住であり、子供たちに説明するときにこの書き方を使っているからです。

その他、 $\lbrack$ と $\rbrack$ などを使う場合もあると思いますが、学校のやり方に従って適当に読み替えてください。

このとき、ベクトル $\overrightarrow{a}$ と $\overrightarrow{b}$ の内積を次のように定義します。

\overrightarrow{a} \cdot \overrightarrow{b} = a_1 b_1 + a_2 b_2

内積はスカラ量として得られます。

3 次元のベクトルの場合には、次のようになります。

ベクトル $\overrightarrow{a} = \langle a_1, a_2, a_3 \rangle$ とベクトル $\overrightarrow{b} = \langle b_1, b_2, b_3 \rangle$ の内積は次の式で定義されます。

\overrightarrow{a} \cdot \overrightarrow{b} = a_1 b_1 + a_2 b_2 + a_3 b_3

こちらも $x$ 成分、 $y$ 成分、 $z$ 成分をそれぞれ掛け合わせて、足しただけです。

こんな数を定義すると、一体どんな良いことがあるのでしょうか？

内積の性質と意味をみていきましょう。

計算の公式

あとでちょくちょく使うので、計算のルールを確認しておきましょう。

まずは交換則がなりたちます。内積の掛ける順番を変えても同じです。

\overrightarrow{a} \cdot \overrightarrow{b} = \overrightarrow{b} \cdot \overrightarrow{a}

定義から $\overrightarrow{a} \cdot \overrightarrow{b} = a_1 b_1 + a_2 b_2$ で、スカラの積の順番は入れ替えられるので明らかですね。

次にスカラ倍の計算です。 $k$ をスカラの定数として、

( k\overrightarrow{a} \cdot \overrightarrow{b} ) = k (\overrightarrow{a} \cdot \overrightarrow{b} )

こちらも $( k\overrightarrow{a} \cdot \overrightarrow{b} ) = k a_1 b_1 + k a_2 b_2 = k ( a_1 b_1 + a_2 b_2 )$ からわかります。

分配法則も成り立ちます。

( \overrightarrow{a} + \overrightarrow{b} ) \cdot \overrightarrow{c} =\overrightarrow{a} \cdot \overrightarrow{c} + \overrightarrow{b} \cdot \overrightarrow{c}

こちらも計算して確かめておきましょう。 $\overrightarrow{c} = \langle c_1, c_2 \rangle$ とすると、 $\overrightarrow{a} + \overrightarrow{b} = \langle a_1 + b_1, a_2 + b_2 \rangle$ ですから、

\begin{aligned} ( \overrightarrow{a} + \overrightarrow{b} ) \cdot \overrightarrow{c} &= ( a_1 + b_1 ) c_1 + ( a_2 + b_2 ) c_2\\ &= a_1 c_1 + b_1 c_1 + a_2 c_2 + b_2 c_2\\ &= a_1 c_1 + a_2 c_2 + b_1 c_1 + b_2 c_2\\ &= \overrightarrow{a} \cdot \overrightarrow{c} + \overrightarrow{b} \cdot \overrightarrow{c} \end{aligned}

$\| \overrightarrow{a} \| = \sqrt{ \overrightarrow{a} \cdot \overrightarrow{a} }$ ノルムは内積の平方根

\| \overrightarrow{a} \| = \sqrt{ \overrightarrow{a} \cdot \overrightarrow{a} }

$\overrightarrow{a}$ と $\overrightarrow{a}$ の内積を計算すると、内積の定義から

\begin{aligned} \overrightarrow{a} \cdot \overrightarrow{a} &= a_1^2 + a_2^2 \\ \end{aligned}

となります。ベクトルの成分とノルム (長さ) は次のような関係にあります。

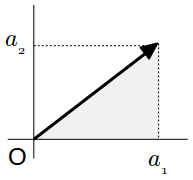
したがって、

\begin{aligned} \| \overrightarrow{a} \| &= \sqrt{ a_1^2 + a_2^2 } \\ &= \sqrt{ \overrightarrow{a} \cdot \overrightarrow{a} } \end{aligned}

となります。

この結果から直ちに $\| \overrightarrow{a} \|^2 = \overrightarrow{a} \cdot \overrightarrow{a}$ とも書けます。

記号 $\| \overrightarrow{a} \|$ はベクトル $\overrightarrow{a}$ のノルム (ベクトルの長さ) を表しています。

$\overrightarrow{a} \cdot \overrightarrow{b} = \| \overrightarrow{a} \| \| \overrightarrow{b} \| \cos \theta$ は余弦定理から

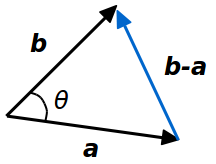
\overrightarrow{a} \cdot \overrightarrow{b} = \| \overrightarrow{a} \| \| \overrightarrow{b} \| \cos \theta

上図のようにベクトル $\overrightarrow{a}$ の終点からベクトル $\overrightarrow{b}$ の終点に向かうベクトルを考ると、これは $\overrightarrow{b} - \overrightarrow{a}$ と表されます。

$\overrightarrow{a}$ の終点からベクトル $\overrightarrow{b}$ の終点に向かうベクトルを $\overrightarrow{c}$ とおくと、同じ始点からの矢印のつながりを考えると $\overrightarrow{a} + \overrightarrow{c} = \overrightarrow{b}$ となるので、 $\overrightarrow{c} = \overrightarrow{b} - \overrightarrow{a}$ がわかります。「終点から終点はこう書く」みたいに丸暗記していたら、時間が経てば忘れて $\overrightarrow{b} - \overrightarrow{a}$ か $\overrightarrow{a} - \overrightarrow{b}$ でわからなくなってしまいます。

丸暗記せずに、なるべくいつも導くようにしましょう。

ベクトル $\overrightarrow{a}$ と $\overrightarrow{b}$ のなす角を $\theta$ とすると、余弦定理から、

\| \overrightarrow{b} - \overrightarrow{a} \|^2 = \| \overrightarrow{a} \|^2 + \| \overrightarrow{b} \|^2 - 2 \| \overrightarrow{a} \| \| \overrightarrow{b} \| \cos \theta

となります。

ここで左辺のノルムを計算すると、

\begin{aligned} \| \overrightarrow{b} - \overrightarrow{a} \|^2 &= ( \overrightarrow{b} - \overrightarrow{a} ) \cdot ( \overrightarrow{b} - \overrightarrow{a} ) \\ &= ( \overrightarrow{b} - \overrightarrow{a} ) \cdot \overrightarrow{b} - ( \overrightarrow{b} - \overrightarrow{a} ) \cdot \overrightarrow{a}\\ &= \overrightarrow{b} \cdot \overrightarrow{b} - \overrightarrow{a} \cdot \overrightarrow{b} - \overrightarrow{b} \cdot \overrightarrow{a} + \overrightarrow{a} \cdot \overrightarrow{a}\\ &= \| \overrightarrow{a} \|^2 + \| \overrightarrow{b} \|^2 - 2 ( \overrightarrow{a} \cdot \overrightarrow{b} ) \end{aligned}

よって、元の式に代入すると、次のように整理できます。

\begin{aligned} \| \overrightarrow{a} \|^2 + \| \overrightarrow{b} \|^2 - 2 ( \overrightarrow{a} \cdot \overrightarrow{b} ) &= \| \overrightarrow{a} \|^2 + \| \overrightarrow{b} \|^2 - 2 \| \overrightarrow{a} \| \| \overrightarrow{b} \| \cos \theta \\ \therefore \quad \overrightarrow{a} \cdot \overrightarrow{b} &= \| \overrightarrow{a} \| \| \overrightarrow{b} \| \cos \theta \end{aligned}

図形で意味を理解する

上の結果で得た次の式の意味を考えてみましょう。

\overrightarrow{a} \cdot \overrightarrow{b} = \| \overrightarrow{a} \| \| \overrightarrow{b} \| \cos \theta

上式の右辺の $\| \overrightarrow{b} \| \cos \theta$ は、下図で赤で示した長さになります。

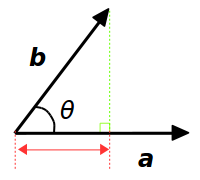
「え、どうして？」と思ったら「三角関数に慣れる (1)」を復習しましょう。

ここで、もし $\overrightarrow{a}$ が座標軸の基本ベクトルであったら $\| \overrightarrow{a} \| = 1$ なので、 $\overrightarrow{a} \cdot \overrightarrow{b} = \| \overrightarrow{a} \| \| \overrightarrow{b} \| \cos \theta = \| \overrightarrow{b} \| \cos \theta$ です。

つまり、基本ベクトルと任意のベクトルの内積を計算することは、その基本ベクトルが示す座標軸への正射影の長さを求めることになります。

以上、ベクトルの内積について説明しました。