ベクトルの発散 div

ベクトルの発散とは？

ベクトル場 $\overrightarrow{F} = F_1(x,y,z)\overrightarrow{i} + F_2(x,y,z)\overrightarrow{j} + F_3(x,y,z)\overrightarrow{k}$ があるとき、次の値を発散 (divergence) といいます。

\text{div} \overrightarrow{F} = \frac{\partial F_1}{\partial x} + \frac{\partial F_2}{\partial y} + \frac{\partial F_3}{\partial z}

$\nabla$ を用いて書くと、形式的にベクトル $\Big\langle\displaystyle\frac{\partial}{\partial x}, \displaystyle\frac{\partial}{\partial y}, \displaystyle\frac{\partial}{\partial z}\Big\rangle$ と $\langle F_1, F_2, F_3\rangle$ との内積を計算するように、成分毎に演算子を作用させることで、次のようにかけます。

\begin{aligned} \nabla \cdot \overrightarrow{F} &= \Big\langle\frac{\partial}{\partial x}, \frac{\partial}{\partial y}, \frac{\partial}{\partial z}\Big\rangle \cdot \langle F_1, F_2, F_3\rangle \\ &= \frac{\partial F_1}{\partial x} + \frac{\partial F_2}{\partial y} + \frac{\partial F_3}{\partial z} \\ &= \text{div} \overrightarrow{F} \end{aligned}

$\langle a, b, c\rangle$ という書き方は、ベクトルの成分表示です。 $a\overrightarrow{i}+b\overrightarrow{j}+c\overrightarrow{k}$ と同じです。

問題 $\overrightarrow{r} = x \overrightarrow{i} + y \overrightarrow{j} + z \overrightarrow{k}$ のとき $\nabla \cdot \overrightarrow{r}$ を求めよ。

解き方上の定義に当てはめると $F_1 = x, F_2 = y, F_3 = z$ だから、それぞれの偏微分は次の通り。

\frac{\partial F_1}{\partial x} = 1, \ \frac{\partial F_2}{\partial y} = 1, \ \frac{\partial F_3}{\partial z} = 1

従って $\overrightarrow{r}$ の発散 $\nabla \cdot \overrightarrow{r}$ は次のように求められます。

\begin{aligned} \nabla \cdot \overrightarrow{r} &= \frac{\partial F_1}{\partial x} + \frac{\partial F_2}{\partial y} + \frac{\partial F_3}{\partial z}\\ &= 1 + 1 + 1\\ &= 3 \end{aligned}

発散の物理的な意味は「単位時間、単位体積からの流出量」

それでは上で定義した発散に、どんな意味があるのか考えてみましょう。

そのために、水が溜められているプールの中を考えます。プールの中には、水が注がれる場所、流れ出る排水口などいろいろあって、場所によって水の速度が違います。

そこで、プールの中に $xyz$ 直交座標系を考えて、場所による速度 $\overrightarrow{v}$ を次のように書きましょう。

$\overrightarrow{v} (x,y,z) = v_1(x,y,z) \overrightarrow{i} + v_2(x,y,z) \overrightarrow{j} + v_3(x,y,z) \overrightarrow{k}$

ここで $\overrightarrow{i}$ 、 $\overrightarrow{j}$ 、 $\overrightarrow{k}$ はそれぞれ、 $x, y, z$ 軸の基本ベクトルです。

さて、水の中に次のように直方体の領域を考えます。 $x, y, z$ 軸方向の長さはそれぞれ、 $\Delta x, \Delta y, \Delta z$ とします。

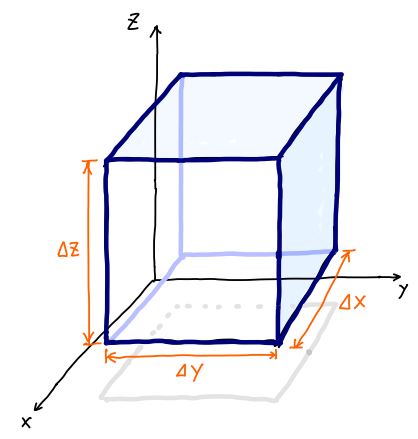
そこで、この領域から単位時間に流出する水の量を計算してみましょう。

そのためにまず、 $x$ 軸に垂直な面に着目します。

まず、この面の面積 $S$ は、縦 $\Delta z$ 、横 $\Delta y$ ですから、 $S=\Delta y\Delta z$ です。これが、 $x$ 座標の前後 $-\displaystyle\frac{\Delta x}{2}$ と $\displaystyle\frac{\Delta x}{2}$ のところにあります。

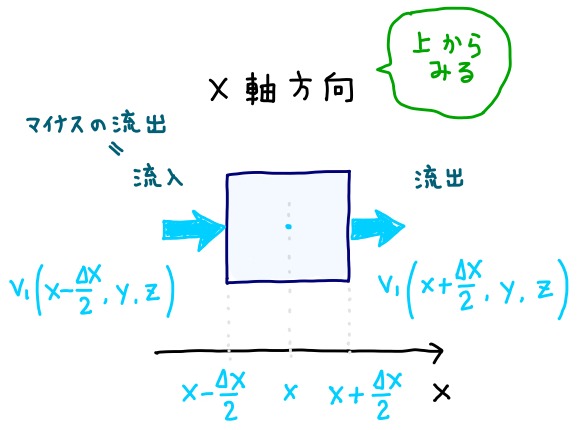
$x$ 座標が $x+\displaystyle\frac{\Delta x}{2}$ のところにある側の面では、 $x$ 方向の速さは $v_1(x+\displaystyle\frac{\Delta x}{2}, y, z)$ ですから、

$\text{\small{流出量}} = v_1(x+\frac{\Delta x}{2}, y, z) \Delta y \Delta z$

また $x$ 座標が $x-\displaystyle\frac{\Delta x}{2}$ のところにある側の面では、 $x$ 方向の速さは $v_1(x-\displaystyle\frac{\Delta x}{2}, y, z)$ ですから、

$\text{\small{流入量}} = v_1(x-\frac{\Delta x}{2}, y, z) \Delta y \Delta z$

従って、 $x$ 軸方向の流出量は差し引きで次のようにかけます。

$\begin{aligned} \text{\small{x 方向の流出量}} &= v_1\Big(x+\frac{\Delta x}{2}, y, z\Big) \Delta y \Delta z - v_1\Big(x-\frac{\Delta x}{2}, y, z\Big) \Delta y \Delta z\\ &= \Big\{v_1\Big(x+\frac{\Delta x}{2}, y, z\Big) - v_1\Big(x-\frac{\Delta x}{2}, y, z\Big) \Big\} \Delta y \Delta z\\ &= \Big[\Big\{v_1 + \frac{\partial v_1}{\partial x}\frac{\Delta x}{2}\Big\} - \Big\{v_1 + \frac{\partial v_1}{\partial x}\Big(-\frac{\Delta x}{2}\Big)\Big\}\Big] \Delta y \Delta z\\ &= \frac{\partial v_1}{\partial x} \Delta x \Delta y \Delta z \end{aligned}$

$y$ 軸方向、 $z$ 軸方向も同様の考え方で、

$\begin{aligned} \text{\small{y 方向の流出量}} &= \frac{\partial v_2}{\partial y} \Delta x \Delta y \Delta z\\ \text{\small{z 方向の流出量}} &= \frac{\partial v_3}{\partial z} \Delta x \Delta y \Delta z \end{aligned}$

よって、上記の微小領域からの単位時間の流出量はこれらを足し合わせて、次のようにかけます。

$\text{\small{単位時間の流出量}} = \Big(\frac{\partial v_1}{\partial x} + \frac{\partial v_2}{\partial y} + \frac{\partial v_3}{\partial z} \Big) \Delta x \Delta y \Delta z$

両辺を、領域の体積 $\Delta x \Delta y \Delta z$ で割ることによって、次がわかります。

$\text{\small{単位時間単位体積からの流出量}} = \frac{\partial v_1}{\partial x} + \frac{\partial v_2}{\partial y} + \frac{\partial v_3}{\partial z}$

これが、ベクトルの発散 $\nabla \cdot \overrightarrow{v}$ の意味です。