逆関数の微分公式
逆関数の微分公式は次の通りです。
この公式はどういう意味でしょうか。少し考えてみましょう。
逆関数の導関数の公式の意味
関数 \(f(x)\) とその逆関数 \(f^{-1}(x)\) の関係をおさらいしておきましょう。
\(y=f(x)\) のグラフが与えられた時、\(y=f^{-1}(x)\) のグラフは下の図のように \(y=x\) に対して対象になります。
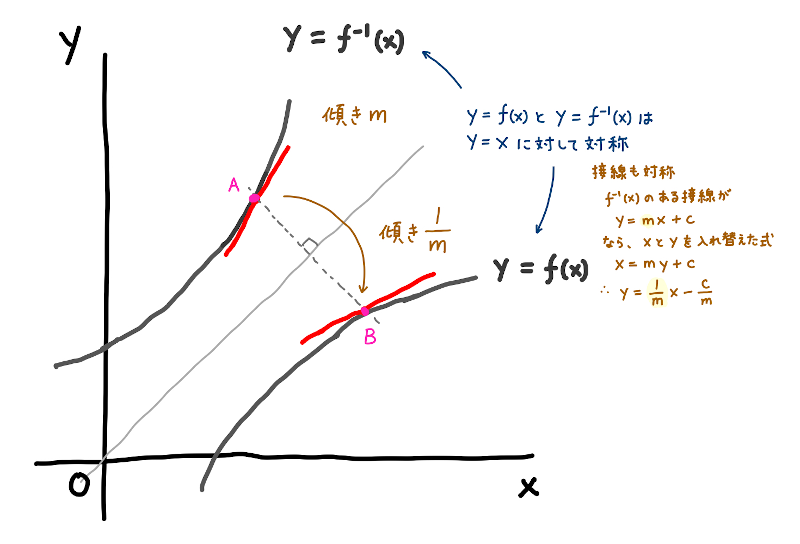
\(y=f^{-1}(x)\) 上に点A をとります。点A の \(y=x\) に対して対象な場所にある \(y=f(x)\) 上の点を 点B とします。
点A での \(y=f^{-1}(x)\) の接線の傾きを \(m\) とすると、点B での \(y=f(x)\) の接線の傾きは \(\displaystyle\frac{1}{m}\) になります。
一般に導関数は接線の傾きを表していますので、点Aでの\(x\)座標を \(x_{A}\) とすると、\(m=(f^{-1})'(x_{A})\) です。
同様に点Bの\(x\)座標を \(x_{B}\) とすると、\(f'(x_{B})=\displaystyle\frac{1}{m}\) です。
これらの関係から、次がわかりました。
\[ \tag{1} (f^{-1})'(x_{A}) = \frac{1}{f'(x_{B})} \]
ちなみに、今は単純化して考えてますので、\(f'(x_{B}) \ne 0\) などの条件は書いてませんが、割り算するには必要な条件ですので含まれていると思ってください。
ここで下の図から、 \(x_B = f^{-1}(x_A)\) の関係があります。
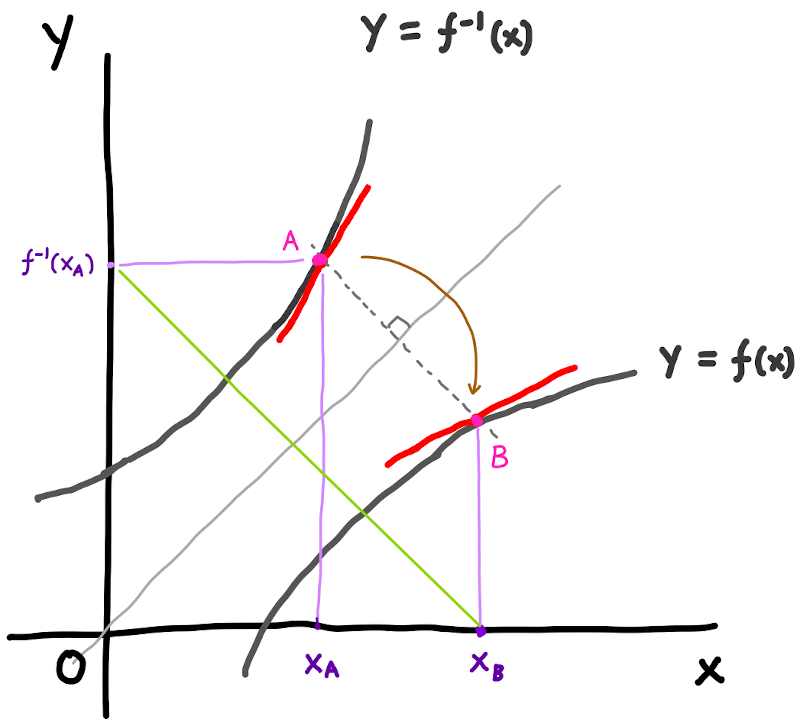
よって上の式1 に \(x_B = f^{-1}(x_A)\) を代入すると次の式を得ます。
\[ (f^{-1})'(x_{A}) = \frac{1}{f'(f^{-1}(x_A))} \]
ここで \(x_A\) は元々任意の点で考えていましたから、\(x\) に書き換えると次の公式になります。
\[ (f^{-1})'(x) = \frac{1}{f'(f^{-1}(x))} \]
公式を丸暗記すると忘れてしまって困ることになるので、さっと図を描いて思い出せる(導き直せる)ようにしておくとテストの時などには役に立つでしょう。
例題を解いて、理解を深めましょう。