ラプラス変換の第二移動法則
単位階段関数
ここでは次のようなグラフを考えます。
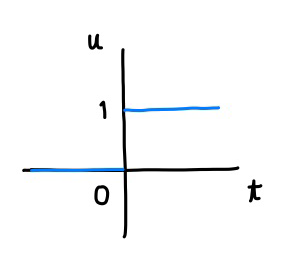
横軸 (t 軸) の 0 より小さいときに値は 0、0 より大きい時は 1 になっています (0 では未定義)。
このグラフは原点を境に左右に 0 から 1 に階段状に変わります。
式で書くと次のようになります。
このように定義される関数 \(u(t)\) を単位階段関数 (unit step function) といいます。 値 0 から原点で階段状に値 1 へとポンと上がっているので「階段」(ステップ) 関数です。
これはヘビサイド関数 (Heaviside function) とも呼ばれます。
平行移動は \( u(t-a) \)
さて、単位階段関数を \(t\) 軸方向に \(a\) だけ移動した場合を考えてみましょう。 \(t = a\) のところに階段ができている場合です。
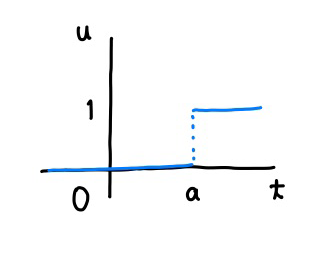
\(t\) 方向への平行移動なので \(u(t - a)\) ですね。\(t = a\) で \(u(0)\) なので、そこに階段ができます。
この形で覚えておいた方が何かと便利です。
ラプラス変換の第二移動法則
なぜ、いきなり単位階段関数がでてきたのかというと、それは平行移動した関数のラプラス変換を考えるためです。
元の関数 \(f(t)\) のラプラス変換を \(F(s)\) とします。そのとき、\(t\) 軸方向に \(a\) だけ平行移動した関数 \(f(t-a)\) のラプラス変換はどうなるか?という話です。
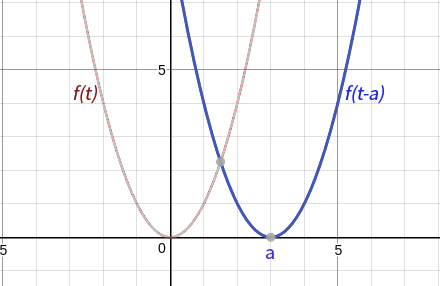
この時、ラプラス変換が存在するのは \([0, \infty)\) です。\(f(t)\) を \(a\) だけ移動したあとも、もともと \([0, \infty)\) であった部分のグラフだけを考えます。
そのために、\(a\) より小さい部分が 0、それ以上が 1 となる単位階段関数 \(u(t-a)\) を、\(f(t-a)\) に掛けた関数 \(u(t-a)f(t-a)\) を考えます。
単位階段関数でマスクするイメージです。
ここでは計算をしませんが、ラプラス変換の定義に入れて計算すると、実はこれは次のような簡単な式になります。
すなわち、t 軸方向に \(a\) だけ平行移動した関数 \(f(t-a)\) のラプラス変換は、元の \(f(t)\) のラプラス変換 \(F(s)\) に \(e^{-as}\) をかけたものになります。
これは特に 第二移動法則 といいます。
次のラプラス変換を求めよ。
\(\mathcal{L}[(t-1) u(t-1)]\)
移動する前の関数を見つけて、それをラプラス変換するところがポイントです。t 関数の並行移動は s 関数に \(e^{-at}\) をかければいいのです。
\(f(t) = t\) とすると \(f(t-1) = t-1\) は、\(f(t)\) を \(t\) 軸方向に \(1\) だけ移動したものです。 よって、\(f(t) = t\) のラプラス変換を \(F(s) = \mathcal{L}[f(t)] \) とすると、求めるラプラス変換 (s 式) は \(e^{-s} F(s)\) になります。
ラプラス変換表から、\(t\) のラプラス変換は
\[ \mathcal{L}[t] = \frac{1}{s^2} \]
ですから、求める答えはこれに \(e^{-s}\) をかけて得られます。
\[ \mathcal{L}[(t-1)u(t-1)] = \frac{e^{-s}}{s^2} \]
このように、 \(f(t)\) を \(t\) 軸方向に \(a\) だけ移動した \(t\) 関数 \(f(t-a)\) のラプラス変換は、\(f(t)\) のラプラス変換 \(F(s)\) に \(e^{-as}\) をかけて求めることができます。
もう一問、例題をみてみましょう。
\(\mathcal{L}[t^2 u(t-1)] \)
単位階段関数で 1 だけ移動していますが、どのような \(t\) 関数を 1 だけ移動したら \(t^2\) になるか注意して考えましょう。
\(t^2\) を \((t-1)\) を括り出すように変形すると次のようになる。
\[ \begin{aligned} t^2 &= [(t-1) + 1]^2\\ &= (t-1)^2 + 2(t-1) + 1 \end{aligned} \]
したがって、問題の式は次のように書き直せる。
\[ \mathcal{L}[t^2 u(t-1)] = \mathcal{L}[ \{(t-1)^2 + 2(t-1) + 1\} u(t-1)] \]
よって第二移動法則から、求める解は \(f(t) = t^2 + 2t + 1\) のラプラス変換を \(F(s)\) としたときに、 \( e^{-s} F(s)\) として求められる。
\[ \begin{aligned} \mathcal{L}[t^2 + 2t + 1] &= \mathcal{L}[t^2] + 2 \mathcal{L}[t] + \mathcal{L}[1]\\ &= \frac{2}{s^3} + 2 \cdot \frac{1}{s^2} + \frac{1}{s} \\ &= \frac{2}{s^3} + \frac{2}{s^2} + \frac{1}{s}\\ \\ \therefore \ \mathcal{L}[t^2 u(t-1)] &= e^{-s}\Big( \frac{2}{s^3} + \frac{2}{s^2} + \frac{1}{s} \Big) \end{aligned} \]
以上、第二移動法則を利用してラプラス変換を求める方法について説明しました。