因数定理

ここでは因数定理 (factor theorem) について説明します。

因数定理 というのは、ある代数方程式 \(P(x) = 0\) が \((x-a)\) なる因数を持つ必要十分条件は \(P(a)=0\) である、ということです。

これだけだと、何を言っているのか分かりにくいかも知れませんが、言っていることは単純です。

因数定理によって、\(x\) の式 \(P(x) = 0\) の \(x\) に \(a\) を代入して、\(P(a) = 0\) となるなら (つまり \(a\) が \(P(x)=0\) の根であれば) 、 \(P(x) = 0\) は \((x-a)\) を因数に持つことがわかります。

「\((x-a)\) を因数に持つ」ということは、「\((x-a)\) と何かの掛け算の形に書き直せる」ということですから、他の \(x\) の式 \(Q(x)\) を使って、\(P(x) = (x-a) \cdot Q(x)\) という形に分解して書けるということです。

さらに他の言い方をすれば、\(P(a) = 0\) となれば、\(P(x)\) は \((x-a)\) で割り切れる、ともいえます。このとき、 \(P(x) = (x-a) \cdot Q(x)\) なら、商は \(Q(x)\) です。

また因数定理ではその逆も正しいと言っていて、もし \(P(x) = (x-a) \cdot Q(x)\) とかけるなら \(P(a)=0\) となると言っています。

ま、これは \(x = a\) としたとき、\((x-a) = 0 \) となるので自明ですね。でも、ともあれ、言っていることはそれだけのことです。

このため、\(P(x)\) を因数分解したいときには \(P(x)=0\) という式を考えてその根 \(a\) を見つければ、因数 \((x-a)\) と \(Q(x)\) に因数分解できることがわかるわけです。

\(P(x) = x^3 + 4x^2 + 3x - 8\) を考えましょう。

たまたま運良く \( x = 1\) としてみたら、\(P(1) = 1 + 4 + 3 - 8 = 0\) となって、\(P(1) = 0\) となることが分かったとします。

となれば、因数定理から \(P(x)\) は \((x-1)\) で割り切れるはずです。やってみましょう。

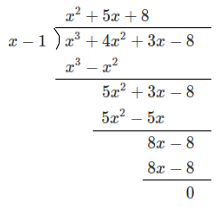
組立て除法でもいいと思いますが、今回は割り算であるというところを強調して上のように書いてみました。

案の定、余り \(0\) となりましたね。これで確かに \(P(x) = (x-1)(x^2+5x+8)\) であることが確認できました。

確かに因数分解できてます。