移動法則のまとめ
さて、ここではラプラス変換で出てくる平行移動を整理しておきましょう。
「移動法則 ~ \(e^{at}f(t) \)のラプラス変換」では、 \(f(t)\) のラプラス変換を \(F(s)\) とすると、\(f(t)\) に \(e^{at}\) をかけてラプラス変換すると \(a\) だけ平行移動して \(F(s-a)\) となることをみました。
\[
\mathcal{L}[e^{at}f(t)] = F(s-a)
\]
これを 第一移動法則 といいます。
また、「ラプラス変換の第二移動法則」では、単位ステップ関数 \(u(t)\) を使って、 \(f(t)\) を \(a\) だけ平行移動してからラプラス変換すると、\(e^{-at}F(s)\) となることをみました。
\[
\mathcal{L}[u(t-a)f(t-a)] = e^{-as}F(s)
\]
こちらは 第二移動法則 といいます。
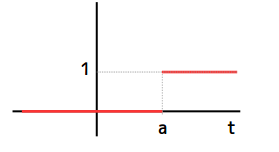
単位ステップ関数は次の通りです。
\[
u (t-a) = \begin{cases}
0 &( t \lt a ) \\
1 &( t \ge a )
\end{cases}
\]
ラプラス変換は \(t\) の関数を \(s\) の関数に変換するわけですが、その変換前に平行移動するか、変換後に平行移動するかというので、 \(e^{-as}\) をかけてあったり \(e^{at}\) がかけてあったりします。
符号が付いたり付かなかったりして、ちょっと混乱しがちかもしれませんが、ラプラス変換前に \(e^{at}\) をかけたら \(s\) 側で平行移動する、 \(t\) 側で平行移動してから変換したら \(e^{-as}\) が付いただけになる ということは覚えておきましょう。