曲率と曲率半径
ここでは「空間曲線がどれだけ曲がっているか」、しっかり数字で表す方法を考えてみましょう。
ある曲線が直線的か曲がっているか、という状態を大まかに把握することは「定性的に」理解するといいます。 どのくらいの量曲がっているかという風に、量をはっきりさせることを「定量的に」理解するという言い方をします。
ここでは空間曲線の曲がり具合を定量的に表す方法を学びます。
曲率半径と曲率
「主法線ベクトルと曲率半径」でみたように、曲線上の2点を通る円を考え、 その円の半径を \(\rho\) とすると次の式が成り立ちます。
\(\rho\) のことを曲率半径 (radius of curvature)といいます。
曲率 (curvature) として \(\kappa = \displaystyle\frac{1}{\rho}\) という値を考えると、次の式になります。
ここで曲率はギリシャ文字のカッパ \(\kappa\) で表しました。
曲率は曲率半径の逆数です。曲線がゆっくり曲がっていれば半径が大きいので曲率は小さくなり、 曲線が急激に曲がっているところは半径が小さくなるので、曲率が大きくなります。
曲率 (=曲がる率) が大きいところが急激に曲がるわけですから、言葉も直感的でわかりやすいですね。
\(\Big| \displaystyle\frac{d\overrightarrow{t}}{ds} \Big|\) というのは、\(s\) に関する単位接線ベクトル \(\overrightarrow{t}\) の変化の大きさですから、 曲がりの多いときには値が大きくなりますし、直線上では \(\overrightarrow{t}\) の変化はないのでゼロになります。
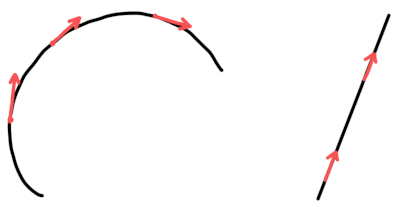
つまり、接線ベクトルの変化の大きさを曲率と呼ぶことによって、空間曲線がどこでどのくらい曲がっているかハッキリした数字を出すことができるようになるのです。