極限値

極限値とは

\(x\) の関数 \(f(x)\) が、点 \(x=a\) を含むある区間で定義されていて、 \(x\)がその区間内を変化して \(a\)に限りなく近付くとします。

このとき、 \(f(x)\)が一定値 \(L\) に限りなく近付くとき、「\(x\)が \(a\) に限りなく近付く時の \(f(x)\) の極限値は \(L\) である」 とか「\(x\)が \(a\) に限りなく近付く時、 \(f(x)\) は \(L\) に収束する」などといいます。

ここで大事なのは、ある点に右側 (大きい方) から近づいても、左側 (小さい方) から近づいても同じ値に収束する、というところがポイントです。

例として、 \(f(x) = x + 1\) の \(x=2\) での極限値を考えてみましょう。

\(x=2\) での極限値はいくつか、というと左側 (\(x \gt 2\)) から \(x=2\) に近付いても、 右側 (\(x \lt 2\)) から近付いても、\(f(x)\) の値は \(3\) に近付きます。

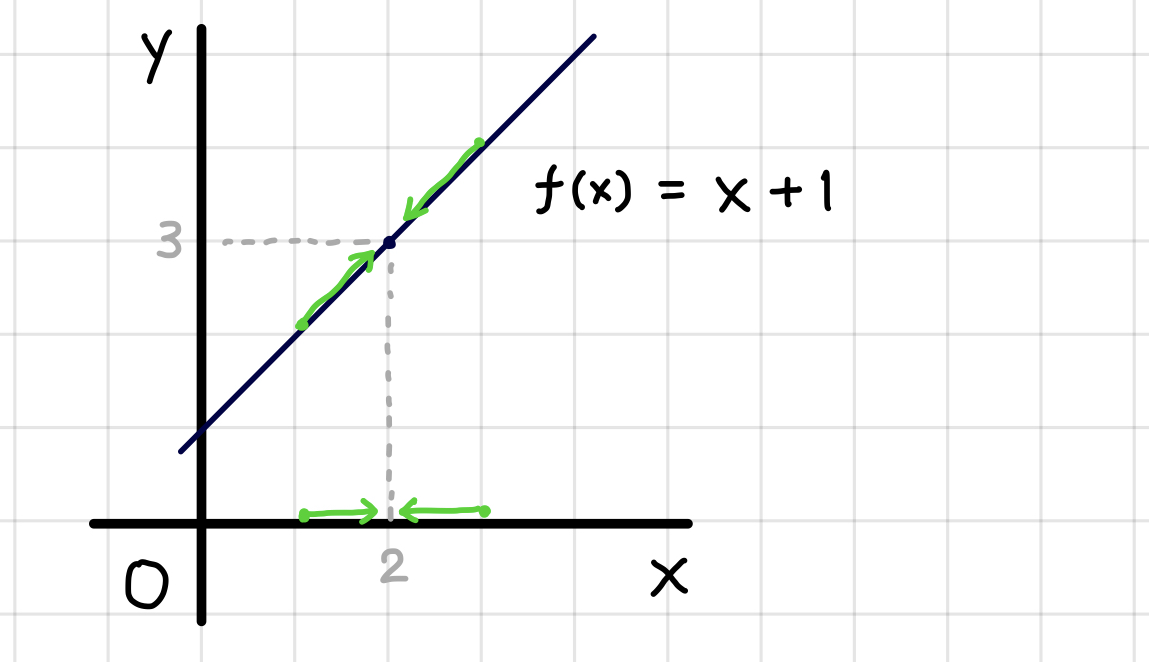
このとき、 \(x=2\) での極限値は \(3\) である、といいます。

ここでは、 \(x=2\) に「近付く」とは言ってますが、\(x=2\) そのものの値ではないので注意が必要です。

例えば、

\[ f(x) = \begin{cases} \ x + 1 & (x \not = 2) \\ \ 5 & (x = 2) \end{cases} \]

という風に、 \(x=2\) のときだけ直線のグラフに乗らないで、ポツンと違う値をとるような関数ではどうでしょうか。

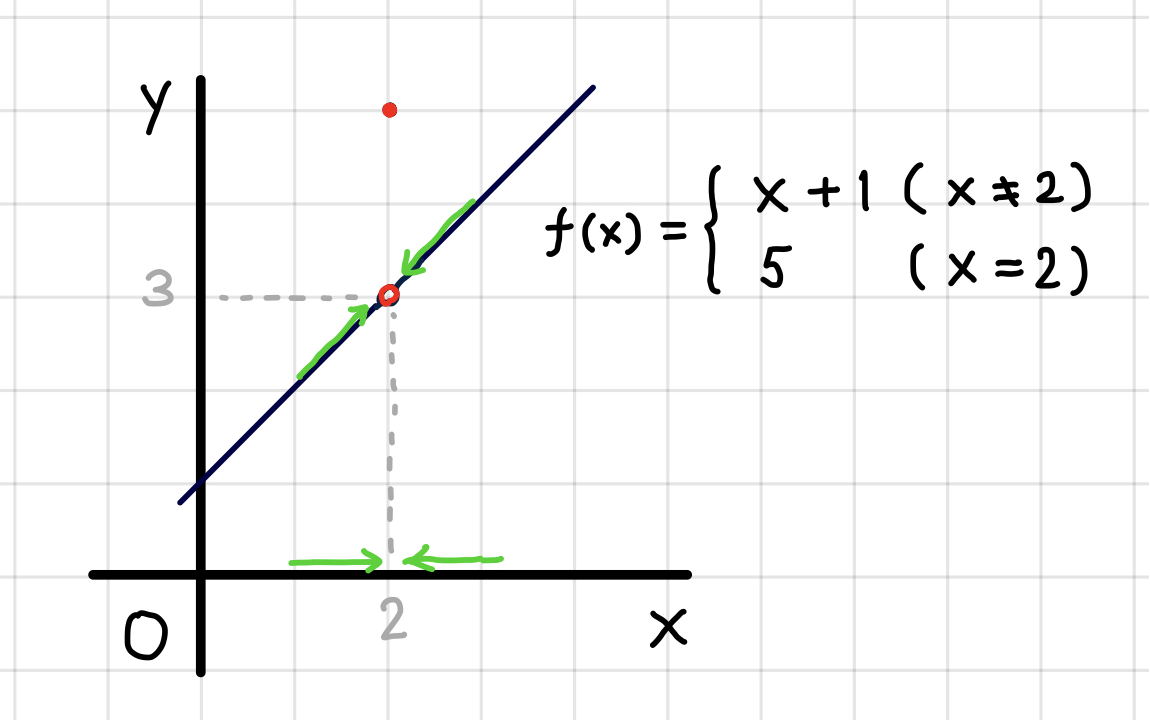
このときも、右側から近付いても、左側から近付いても同じく、 \(f(x)\) は \(3\) に近付きます。 ですから、\(f(x)\) の \(x=2\) のときの極限値は \(3\) である、となります。

記号で書くと、右側から \(x=a\) に近付いたときに \(f(x)\) が \(L\) という一定値に近付くとき

と書きます。これを右側極限値といいます。

同様に、左側から \(x=a\) に近付いたときに \(f(x)\) が \(L\) という一定値に近付くとき

と書きます。これを左側極限値といいます。

右側極限値と左側極限値が違う場合

上のようなキレイなグラフではなく、次のように \(x=a\) でグラフがバラバラになっているような状況もみておきましょう。

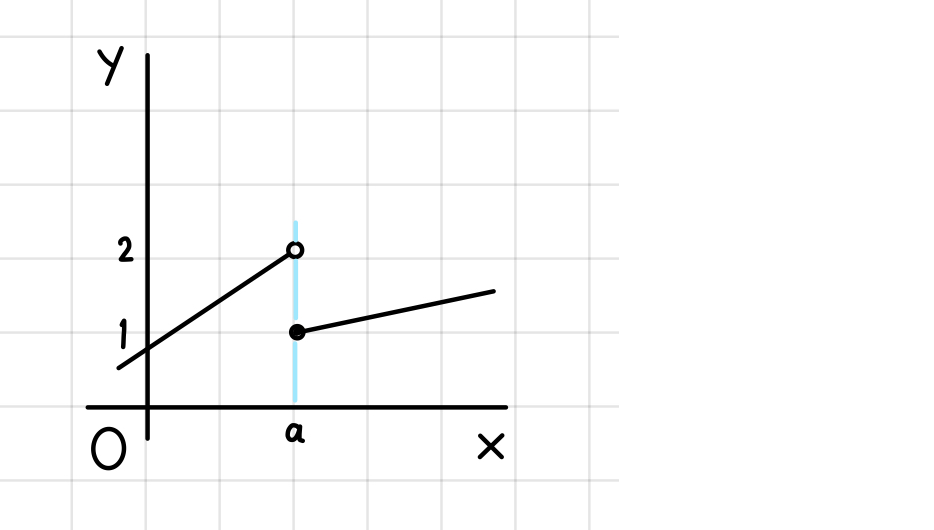
このとき、\(x=a\) に右側から近付いたときには、\(f(x)\) は \(1\) に近付いています。

\[\lim_{a \to a+0} f(x) =1\]

一方、\(x=a\) に左側から近付いた時は、\(f(x)\) は \(2\) に近付いています。

\[\lim_{x \to a-0} f(x) = 2\]

よって、

\[\lim_{x \to a+0} f(x) \not = \lim_{x \to a-0} f(x)\]

ですから、この \(f(x)\) は \(x = a\) での極限値は存在しません。

極限地に関する厳密な証明

ここまで、極限値についてグラフを用いて近付く値を検討しました。 しかし実は厳密には、極限値は \(\delta-\epsilon\)論法という方法で証明されるものです。

もう少し厳密に考えたい方は、「ε-δ 論法による極限」をみてください。