ベクトル積の成分 ~ 行列式の表現
ベクトル \(\overrightarrow{a}\) とベクトル \(\overrightarrow{b}\) のベクトル積 (クロス積) \(\overrightarrow{a} \times \overrightarrow{b}\) の書き方について説明します。
「ベクトル積」は日本語では 外積とも言います。しかしながら、英語の言い方ではベクトル積は "cross product" とか "vector product" と言って、
outer product とは呼ばないので注意が必要です。
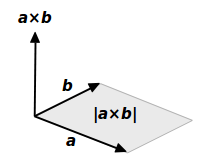
ベクトル \(\overrightarrow{a}\) とベクトル \(\overrightarrow{b}\) の \(x\), \(y\), \(z\) 成分が次の場合を考えます。
\[
\overrightarrow{a} = \langle a_1, a_2, a_3 \rangle
\]
\[
\overrightarrow{b} = \langle b_1, b_2, b_3 \rangle
\]
この時、ベクトル積の成分は次のようになります。
\[
\overrightarrow{a} \times \overrightarrow{b} = \langle a_2 b_3 - a_3 b_2,\enspace a_3 b_1 - a_1 b_3,\enspace a_1 b_2 - a_2 b_1 \rangle
\]
\(x\) 軸、 \(y\) 軸、\(z\) 軸方向の基本ベクトルをそれぞれ 、 \(\overrightarrow{i}\)、\(\overrightarrow{j}\)、\(\overrightarrow{k}\) として書き直すと、次のようにかけます。
\[
\overrightarrow{a} \times \overrightarrow{b} = (a_2 b_3 - a_3 b_2) \overrightarrow{i} + (a_3 b_1 - a_1 b_3) \overrightarrow{j} + (a_1 b_2 - a_2 b_1) \overrightarrow{k}
\]
ベクトル積の行列式表現
ベクトル積の成分は行列式を使って書くとスッキリ覚えられます。行列式を使って次のように書き、1 行目で展開すると上の形になります。
\[
\overrightarrow{a} \times \overrightarrow{b} = \begin{vmatrix}
\overrightarrow{i} & \overrightarrow{j} & \overrightarrow{k} \\
a_1 & a_2 & a_3 \\
b_1 & b_2 & b_3
\end{vmatrix}
\]
「スッキリ書ける」と言われたのに、余計にややこしく見えていたらちょっと切ないので、ここでは念のため書き下しておきます。
この行列式表現から、上の単位ベクトルを使った書き方にするには、この行列式を 1 行目で展開します。
一般にサイズが \(3 \times 3\) の行列 \(A = \{a_{ij}\}\) を 1 行目で展開するということは、余因子 \(C_{ij}\) を使って次のように展開する、ということです。
\[
\det(A) = \begin{vmatrix}
a_{11} & a_{12} & a_{13} \\
a_{21} & a_{22} & a_{23} \\
a_{31} & a_{32} & a_{33} \\
\end{vmatrix} = a_{11} C_{11} + a_{12} C_{12} + a_{13} C_{13}
\]
従って、ベクトル積の行列式を 1 行目で展開すると、小行列式 \(M_{ij}\) を使って次のように書けます。
\[
\begin{aligned}
\overrightarrow{a} \times \overrightarrow{b} &= \overrightarrow{i} \cdot C_{11} + \overrightarrow{j} \cdot C_{12} + \overrightarrow{k} \cdot C_{13}\\
&= \overrightarrow{i} \cdot (-1)^{1+1} M_{11} + \overrightarrow{j} \cdot (-1)^{1+2} M_{12} + \overrightarrow{k} \cdot (-1)^{1+3} M_{13}\\
&= M_{11} \overrightarrow{i} - M_{12} \overrightarrow{j} + M_{13} \overrightarrow{k} \\
&= \begin{vmatrix}
a_2 & a_3\\
b_2 & b_3
\end{vmatrix} \overrightarrow{i} -
\begin{vmatrix}
a_1 & a_3\\
b_1 & b_3
\end{vmatrix} \overrightarrow{j} +
\begin{vmatrix}
a_1 & a_2\\
b_1 & b_2
\end{vmatrix} \overrightarrow{k} \\
&= \begin{vmatrix}
a_2 & a_3\\
b_2 & b_3
\end{vmatrix} \overrightarrow{i} +
\begin{vmatrix}
a_3 & a_1\\
b_3 & b_1
\end{vmatrix} \overrightarrow{j} +
\begin{vmatrix}
a_1 & a_2\\
b_1 & b_2
\end{vmatrix} \overrightarrow{k}
\end{aligned}
\]
ここで、2 項目の符号をマイナスからプラスにするため、行列式では隣り合う列を入れ替えると符号が変わることを使っています。
\(2 \times 2\) 行列はたすき掛けでパッと見てわかるように、次の式に変形できることがわかりますね。
\[
\overrightarrow{a} \times \overrightarrow{b} = (a_2 b_3 - a_3 b_2) \overrightarrow{i} + (a_3 b_1 - a_1 b_3) \overrightarrow{j} + (a_1 b_2 - a_2 b_1) \overrightarrow{k}
\]
以上、ベクトル積の成分を簡便に表示する方法について説明しました。
