空間での平面と法線ベクトル

\(xyz\) 直交座標空間内での平面は、 \(A, B, C, D\) を実数として、次の式で与えられます。

\[ A x + B y + C z + D = 0 \]

このとき、\(x\) 軸、\(y\) 軸、\(z\) 軸の基底ベクトルをそれぞれ \(\overrightarrow{i}\)、\(\overrightarrow{j}\)、\(\overrightarrow{k}\) とすると、法線ベクトル \(\overrightarrow{a}\) は次の式で表されます。

\[ \overrightarrow{a} = A \overrightarrow{i} + B \overrightarrow{j} + C \overrightarrow{k} \]

大きさ \(1\) の単位法線ベクトル \(\overrightarrow{n}\) は、次式で求まります。

\[ \begin{aligned} \overrightarrow{n} &= \frac{\overrightarrow{a}}{\| \overrightarrow{a} \|}\\ &= \frac{ A \overrightarrow{i} + B \overrightarrow{j} + C \overrightarrow{k}}{\sqrt{A^2 + B^2 + C^2}} \end{aligned} \]

どうしてそうなるのでしょうか。

上の式で与えられる平面上に点 \(P(x_o, y_o, z_o)\) と点 \(Q(x, y, z)\) を考えます。点 \(P\) と点 \(Q\) が、上の式で与えられた平面上にあるということは、点 \(P\) と点 \(Q\) の座標が上の式を満たすということです。代入して並べて書くと次のようになります。

\[ \begin{aligned} &A x &+ &B y &+ &C z &+ D &= 0\\ &A x_o &+ &B y_o &+ &C z_o &+ D &= 0 \end{aligned} \]

上の式を引き算すると、次の式が得られます。

\[ \begin{aligned} A (x - x_o) + B (y - y_o) + C (z-z_o) = 0 \end{aligned} \]

この式は \( \overrightarrow{a} = \langle A, B, C \rangle \) と \(\overrightarrow{x} = \langle x - x_o, y - y_o, z - z_o \rangle \) という二つのベクトルを考えると、その内積が \(0\) 、つまり \( \overrightarrow{a} \cdot \overrightarrow{x} = 0 \) であることを示しています。

さて、ここで \(\overrightarrow{x}\) は平面上の任意の二点を始点と終点とするベクトルです。

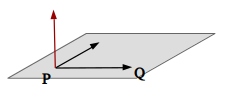
よって、\(\overrightarrow{a}\) は平面上のベクトル \(\overrightarrow{x}\) と垂直であるので、法線ベクトルであることがわかります。