自然対数の底

自然対数の底 \(e\) は ネイピア数あるいは オイラー数 (Euler's number) と呼ばれる定数です。次の式で定義されます。

\[ e = \lim_{n \to \infty} \Big( 1 + \frac{1}{n} \Big)^{n} \]

さてこれを定義として、いくつか大事な式を導いておきましょう。あとでちょこちょこと出てきますので。

まずは、こちら。

\[ e = \lim_{x \to 0} ( 1 + x )^{\frac{1}{x}} \]

これは \(e\) の定義の式で \(n = \displaystyle{\frac{1}{x}}\)、すなわち \(\displaystyle{\frac{1}{n}} = x\) とすると、 \(n \to \infty\) で \(x \to 0\) であることから、直ちにわかります。

次の式を証明せよ。

\[ \lim_{h \to 0} \frac{\ln(1 + h)}{h} = 1 \]

\(\ln x\) は自然対数です。つまり \(e\) を底とする対数関数 \(\log_{e} x = \ln x\) です。

上の定義が分かっていれば単純に式変形するだけです。

\[ \begin{aligned} \lim_{h \to 0} \frac{\ln( 1 + h )}{h} &= \lim_{h \to 0} \frac{1}{h} \cdot \ln(1 + h) \\ &= \lim_{h \to 0} \ln ( 1 + h )^{\frac{1}{h}} \\ &= \ln e \\ &= 1 \end{aligned} \]

\(\displaystyle\frac{\ln( 1 + h )}{h}\) が \( \displaystyle\frac{1}{h} \cdot \ln(1 + h)\) であることに気付かないと、手が止まってしまいますね。 \(\ln\) は対数なので、 \( a \cdot \ln x = \ln x^a\) です。

それと、上で求めておいた \(e\) の定義の \( x \to 0\) バージョンを使えるところに気付くのがポイントです。

\(\ln e = 1\) は \(\ln e = \log_e e\) であることから明らかです。そもそも \(\log_e e\) という数は「底である \(e\) を \(\log_e e\) 乗したら真数である \(e\) になる数」です。 \(e\) を 1 乗したら \(e\) なので、\(\log_e e = 1\) です。

もうひとつ、他でもちょくちょく出てくる式を導いておきましょう。

次の式を証明せよ。

\[ \lim_{x \to 0} \frac{e^x - 1}{x} = 1 \]

上で確認したように次が成り立つ。

\[ \lim_{h \to 0} \frac{\ln(1 + h)}{h} = 1 \]

ここで \( 1 + h = e^x\) とおくと、\(h \to 0\) のとき \( x \to 0\) となる。よって、上式を書き換えると

\[ \begin{aligned} \lim_{x \to 0} \frac{\ln e^x }{e^x - 1} &=\lim_{x \to 0} \frac{x }{e^x - 1} \\ &= \lim_{x \to 0} \frac{1 }{\Big(\displaystyle\frac{e^x - 1}{x} \Big)} \\ &= 1 \end{aligned} \]

よって、

\[ \lim_{x \to 0} \frac{e^x - 1}{x} = 1 \]

最後のところは逆数の極限値が \(1\) であることから、ただちに結論としてもいいです。

グラフで意味を考える

上の式の意味を考えておきましょう。

関数 \(f(x) = e^x\) を考えて \(xy\) 平面で \(y = f(x)\) のグラフを考えます。

\(x = 0\) から \(x\) の微少変化 \(\Delta x = h\) を考えます。このときの \(y\) の微少変化は \(\Delta y = f( h + 0 ) - f(0)\) です。

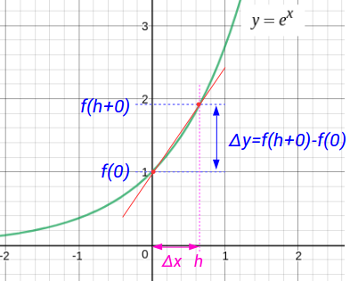
\(x = 0\) での \(y = f(x)\) の接線の傾きは、 \(h\) を限りなく小さくすることで求まります。

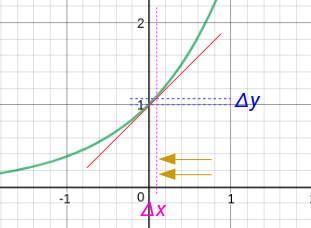
よって

\[ \begin{aligned} (x = 0 \text{\small{での接線の傾き}}) &= \lim_{h \to 0} \frac{\Delta y}{\Delta x}\\ &= \lim_{h \to 0} \frac{f(h) - f(0)}{h}\\ &= \lim_{h \to 0} \frac{e^h - 1}{h} \end{aligned} \]

この値は上で求めた式から \(1\) になります。

よって、上で求めた \(\displaystyle\lim_{x \to 0} \displaystyle\frac{e^x - 1}{x} = 1\) という結果から、 \(y = e^x\) のグラフの \(x = 0\) での接線の傾きが \(1\) であることがわかります。