部分分数分解の手順

ここでは部分分数分解 (partial fraction decomposition) を行う方法を説明します。部分分数分解というのは、次のように式を簡単にすることを言います。

\[ \frac{7x-13}{x^2-2x-3} \xrightarrow{\text{部分分数分解}} \frac{2}{x-3} + \frac{5}{x+1} \]

もう少し正確な言い方だと「ある有理式を多項式と分子の次数が分母の次数より小さい有理式の和で表すこと」 となります。有理式というのは (多項式)/(多項式) で表される式ですね。

微分積分とかラプラス変換とか、いろんな場面で、式を単純にするのによく使われますので、しっかりやり方をマスターしましょう。

それから「部分分数分解」という名前自体についてですが、「部分分数展開」とも良く言われます。

部分分数分解をする手順

はじめに、分子の多項式の次数が分母の多項式の次数より小さいことを確認します。もし、次数が同じか大きければ、式を変形します。

(例1)

\[ \frac{7x-13}{x^2-2x-3} \]

分子 \(7x-13\) の次数は 1 で、分母 \(x^2-2x-3\) の次数は 2 ですから、このままで OK です。

(例2)

\[ \frac{x^2+4x+5}{x+1} \]

分子 \(x^2+4x+5\) の次数は 2 で、分母 \(x+1\) の次数は 1 です。このため次のステップへ進む前に、分子の次数を下げましょう。

やり方は自由ですが、例えば \((x^2+4x+5)\) を \((x+1)\) で割るのに組立除法を使うと・・・

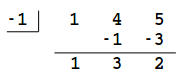
となって \(x^2+4x+5=(x+3)(x+1)+2\) であることがわかるので、次のように変形できます。

\[ \begin{aligned} \frac{x^2+4x+5}{x+1} &= \frac{(x+3)(x+1)+2}{x+1} \\ &= x+3+\frac{2}{x+1} \end{aligned} \]

・・・ま、この例だとこれで終了ですけど・・・ (汗) でも、ま、ポイントは次数をチェックするということです。

次に分母を因数分解します。

(例1)

\[ \frac{7x-13}{x^2-2x-3} = \frac{7x-13}{(x-3)(x+1)} \]

次に部分分数にわけます。このとき、定数 \(A, B, C, \cdots\) を使って以下のように分けていきます。

(例1)

基本は因数毎に分数にわけます。

\[ \frac{7x-13}{(x-3)(x+1)} = \frac{A}{x-3} + \frac{B}{x+1} \]

(例2)

分母の因数の最大次数が \(n \gt 1\) なら、分子の次数は \(n-1\) とします。

\[ \frac{1}{(x+1)(x^2+2)} = \frac{A}{x+1} + \frac{Bx+C}{x^2+1} \]

(例3)

分母が \(n \gt 1\) 乗となっている箇所は、次のように \(1, 2, \cdots, n \) 乗の項を作ります。

\[ \frac{1}{(x+1)^3(x+2)} = \underbrace{ \frac{A}{x+1} + \frac{B}{(x+1)^2} + \frac{C}{(x+1)^3} }_{\small{\text{1乗, 2乗, 3乗}}} + \frac{D}{x+2} \]

上で部分分数に分けましたが、このとき定数 \(A, B, C, \cdots\) を入れ込みました。これらがわかれば、部分分数の出来上がりです。

考え方としては簡単ですが、下手すると計算が煩雑になってしまい、面倒ですし間違いも増えてしまいます。

ここでは分母を払う方法を紹介します。

(例1)

上の例1の両辺に \((x-3)(x+1)\) をかけて分母を払います。すると次のようになります。

\[ \begin{aligned} 7x-13 &= A(x+1) + B(x-3) \end{aligned} \]

これが恒等式となる、つまり \(x\) は何でも成り立つはずなので \(x=-1\) を代入します。

\[ \begin{aligned} 7 \cdot (-1) -13 &= A \cdot 0 + B \cdot (-4) \\ -20 &= B \cdot (-4) \\ B &= 5 \end{aligned} \]

次に \(x=3\) を代入します。

\[ \begin{aligned} 7 \cdot 3 -13 &= A \cdot (3+1) + B \cdot 0 \\ 8 &= A \cdot 4 \\ A &= 2 \end{aligned} \]

以上で \(A=2, B=5\) であることがわかったので、次のように部分分数分解できました。

\[ \begin{aligned} \frac{7x-13}{(x-3)(x+1)} &= \frac{2}{x-3} + \frac{5}{x+1} \end{aligned} \]