指数関数と対数関数の関係

指数関数と対数関数の関係についてみておきましょう。

指数関数 は基本的には「ある数を \(x\) 乗したらいくつになるか」 ということを求めるものですが、通常は特に断りがなければネイピア数 \(e\) を底とする関数のことを指す場合が多いです。

つまり、\(y=2^x\) とかも指数関数ではあるのですが、しばしば「指数関数」といったら、 何を何乗するのか言わなくても、\(e\) を底とする指数関数、つまり、\(y=e^x\) のことになります。

逆に底を \(e\) 以外のモノを考えるなら、「2 を底とする指数関数・・・」とかハッキリ言った方が良いということです。

対数関数の方も、特に断りが無ければ \(e\) を底とする対数を考えます。

\(e\) を底とする対数のことを自然対数といって \(log_{e} x\) を \(\ln x\) と書きます。

グラフを描くと次のようになります。

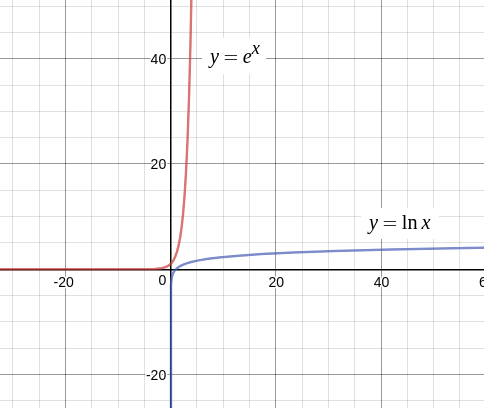
ちなみに、10 を底とする対数は常用対数 といいます。