区分求積法
ここでは定積分を数列の和 (級数) に書き換えたり、逆に級数を定積分に書き換えたりします。
関数 \(f\) が \([a,b]\) で積分可能のとき、次が成り立つ。
\[ \int_a^b f(x) dx = \lim_{n \to \infty} \sum_{i=1}^n f(x_i) \Delta x \]
ここで \(\Delta x = \cfrac{b-a}{n}\)、\(x_i = a + i\Delta x\) とする。
関数 \(f\) が区間 \([a,b]\) で積分可能のとき、上で書いたような級数で定積分の値が求められます。
どんな関数が積分可能なのでしょうか?関数が積分可能であるためには、必ずしも連続でなければいけないことはないのですが、連続な関数であれば積分可能です。
上の定理の意味は、どういうことでしょうか?
適当にグラフを書いて考えてみましょう。
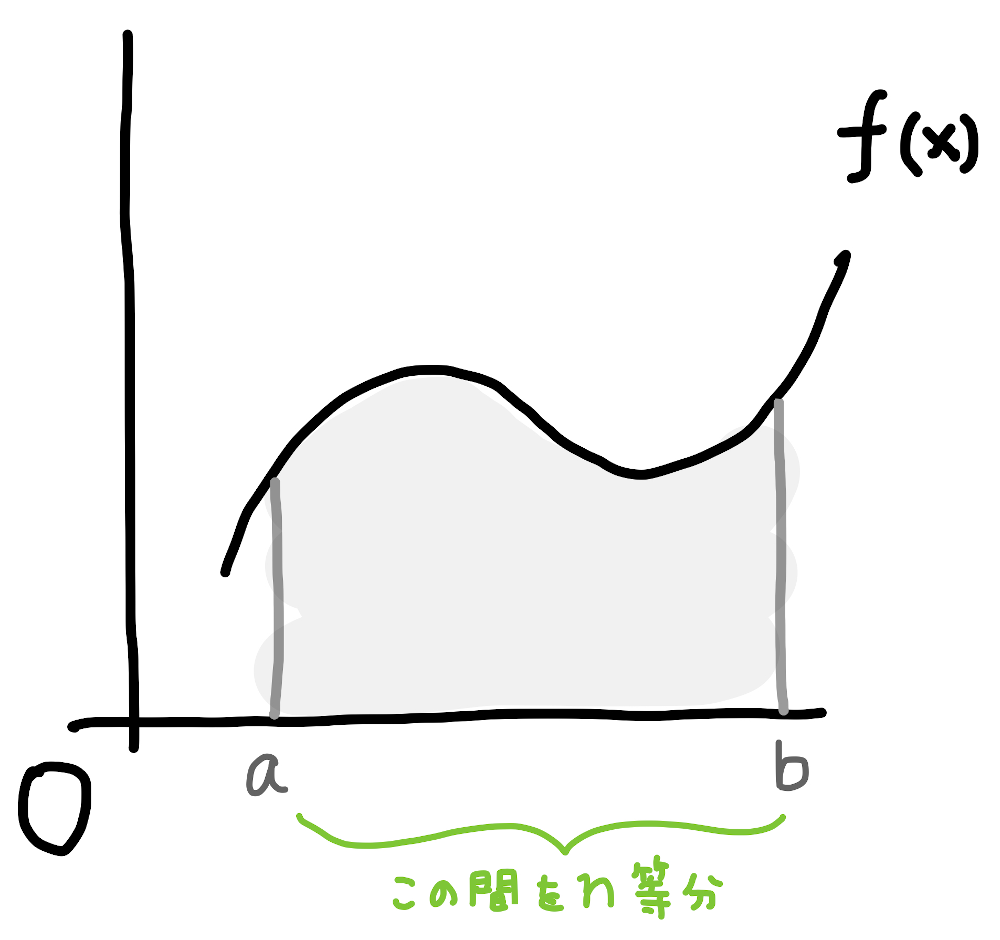
まず閉区間 \([a,b]\) を \(n\) 等分します。
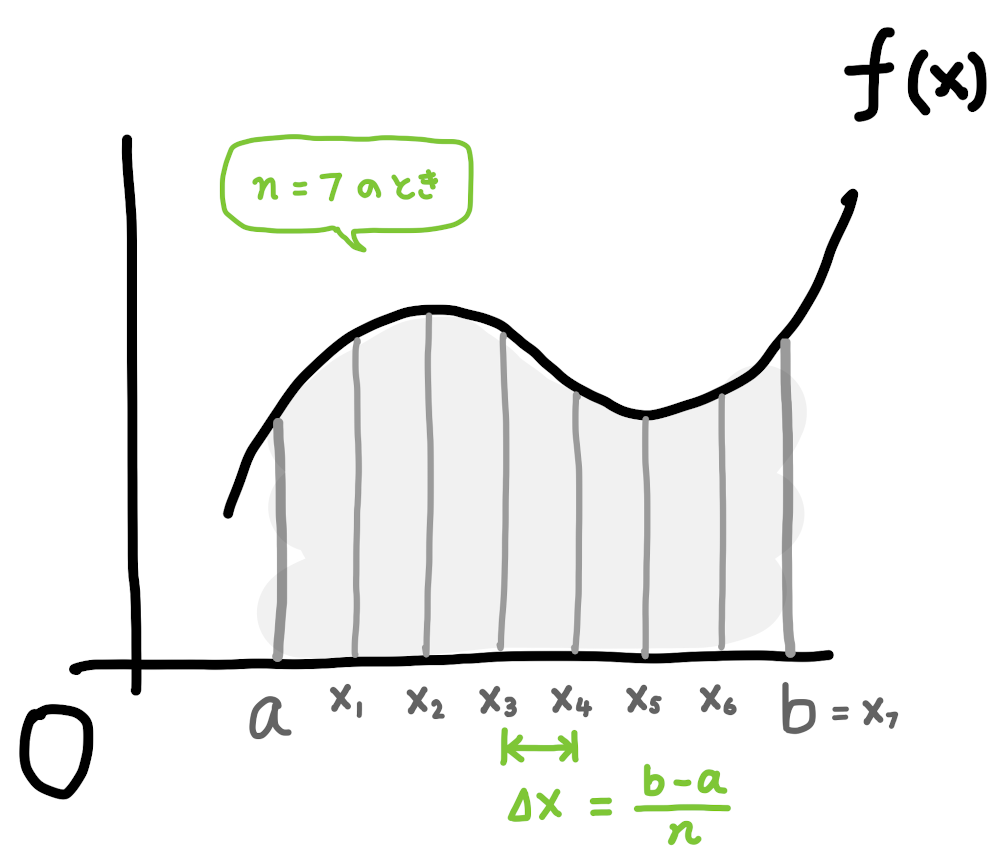
\(a\) から \(b\) までの長さは \(b-a\) ですから、その \(n\) 等分は \(\cfrac{b-a}{n}\) です。これを \(\Delta x\) とおきます。
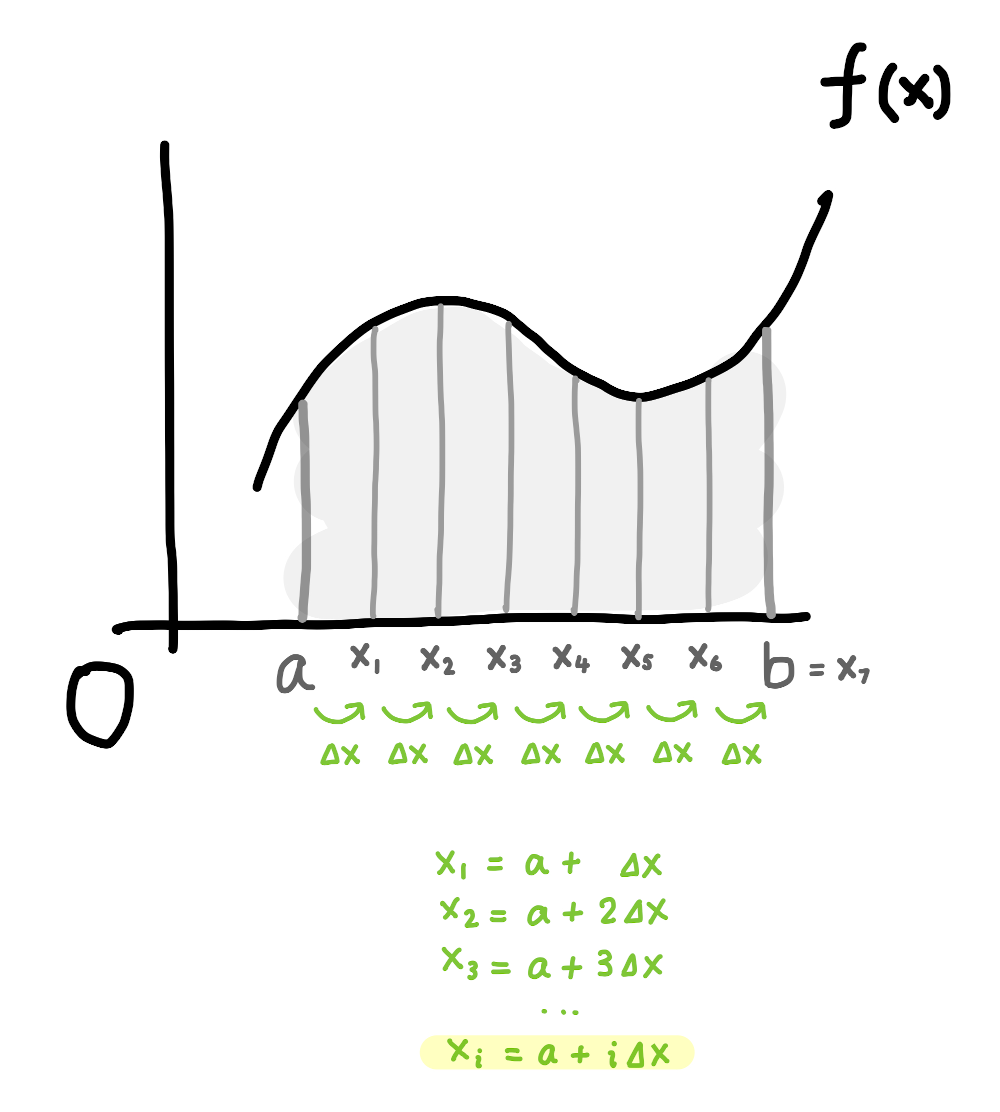
\(x_1\) は \(a\) から \(\Delta x\) だけ進んだ所にあるので、\(x_1 = a + \Delta x\) です。
\(x_2\) は \(a\) から \(2 \Delta x\) だけ進んだ所にあるので、\(x_1 = a + 2 \Delta x\) です。
こう考えてわかるように、 \(i\) 番目 \((i=1, 2, \cdots, n)\) の \(x_i\) は \(x_i = a + i \Delta x\) です。
さて、ここで下の図のように、区間 \([a, b]\) で高さ \(f(x_1), f(x_2), \cdots, f(x_n)\) で幅 \(\Delta x\) の長方形 \(n\) 個を考えます。
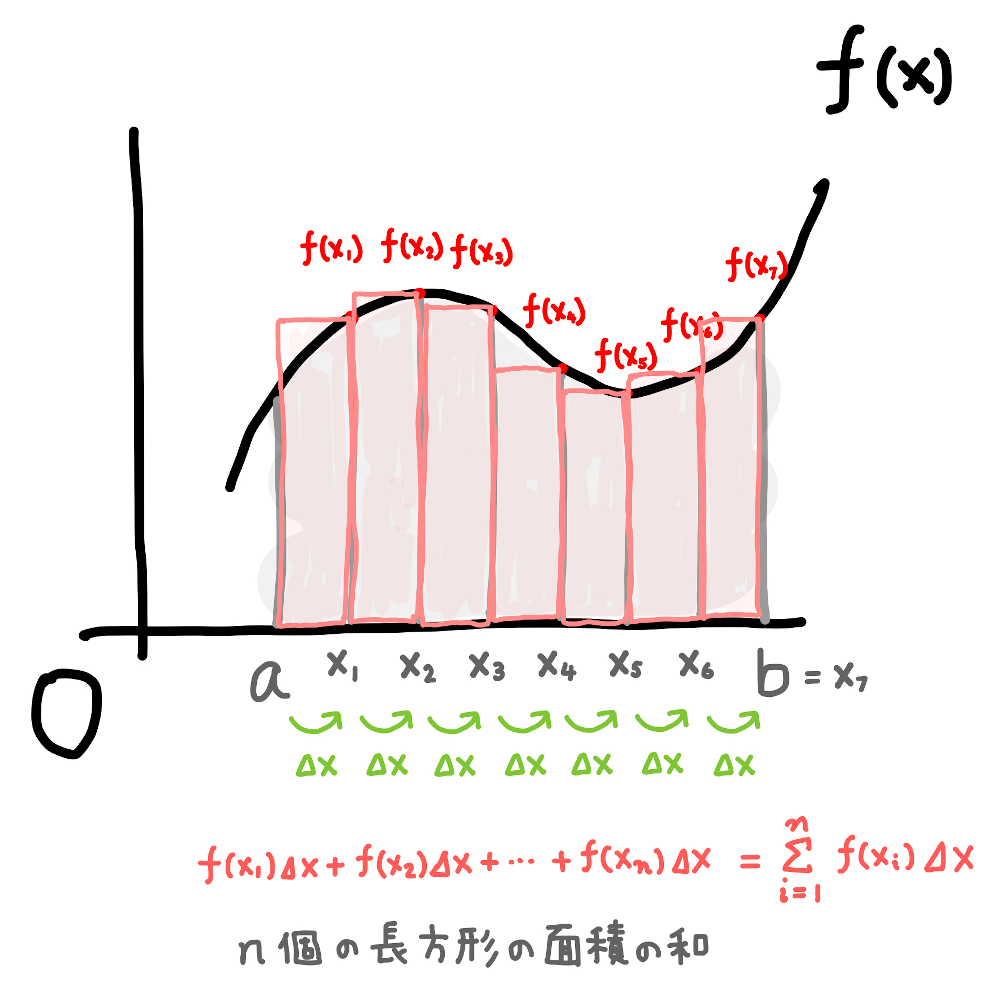
この \(n\) 個の長方形の面積の和は次のようになります。
\[ f(x_1)\Delta x + f(x_2)\Delta x + \cdots + f(x_n) \Delta x = \sum_{i=1}^{n} f(x_i) \Delta x \]
ここで区間 \([a,b]\) の分割数 \(n\) をどんどん大きくします。
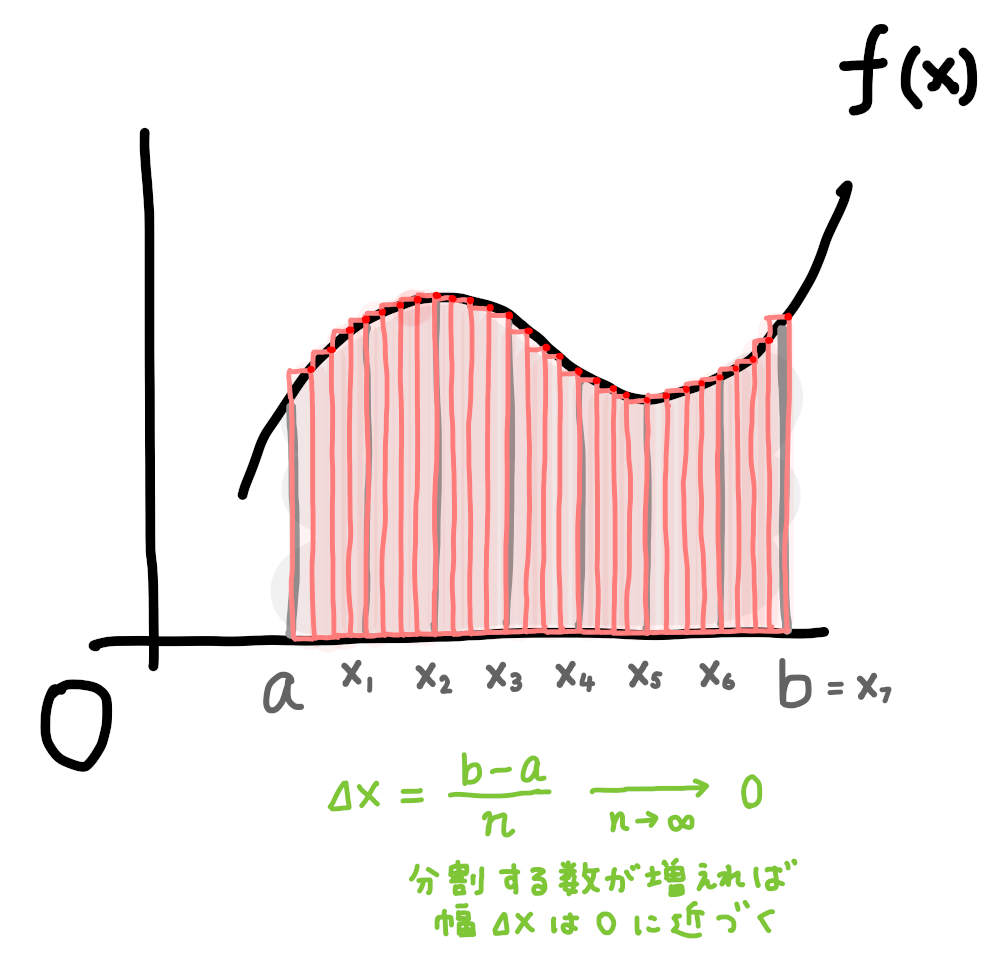
区間の分割数が大きくなれば、それぞれの長方形の幅 \(\Delta x\) は \(0\) に近づきます。
\(n \to \infty\) のときの長方形の和が、関数 \(f\) の \([a,b]\) での定積分に等しい、というのがこの定理の意味です。
このように短冊型の区分の面積を考えて、その分割数の極限値から面積を求める方法を区分求積法といいます。
このように短冊状の長方形の和を リーマン和 (Riemann sum) といいます。リーマン和は分割の仕方に依存して値が変わります。ここでは区間 \([a,b]\) を等間隔に分割して、分割の右端の点で和を考えたことになります。
引き続き、問題を解いてみましょう。